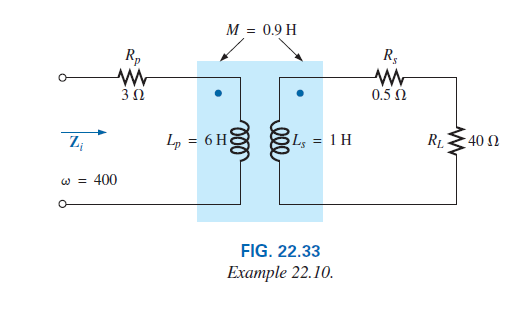
Question 22.10: Determine the input impedance to the air-core transformer in...

Z _{i}= Z _{p}+\frac{(\omega M)^{2}}{ Z _{s}+ Z _{L}}.

=R_{p}+j X_{L_{p}}+\frac{(\omega M)^{2}}{R_{s}+j X_{L_{s}}+R_{L}}.

=3 \Omega+j 2.4 k \Omega+\frac{((400 rad / s )(0.9 H ))^{2}}{0.5 \Omega+j 400 \Omega+40 \Omega}.

\cong j 2.4 k \Omega+\frac{129.6 \times 10^{3} \Omega}{40.5+j 400}.

=j 2.4 k \Omega+\underbrace{322.4 \Omega \angle-84.22^{\circ}}_{\text {capacitive }}.

=j 2.4 k \Omega+(0.0325 k \Omega-j 0.3208 k \Omega).

=0.0325 k \Omega+j(2.40-0.3208) k \Omega.

\text { and } Z_{i}=R_{i}+j X_{L_{i}}=32.5 \Omega+j 2079 \Omega=2079.25 \Omega \angle 89.10^{\circ}.