Question 18.3: Determine the reactions and the member end forces for the fr...
Determine the reactions and the member end forces for the frame shown in Fig. 18.13(a) by using the matrix stiffness method.

Learn more on how we answer questions.
Degrees of Freedom From the analytical model of the frame shown in Fig. 18.13(b), we observe that while joints 1 and 3 of the structure can neither translate nor rotate, joint 2 is free to translate as well as rotate. Thus the frame has three degrees of freedom: the translations d_1 and d_2 in the X and Y directions, respectively, and the rotation d_3 of joint 2.
Structure Stiffness Matrix
Member 1 Since the local xy coordinate system for this member coincides with the global XY coordinate system, no coordinate transformations are needed; that is, the member stiffness relations in the local and global coordinates are the same. By substituting E = 201.4 kPa, I = 0.039 m^4, A = 1111 cm², and L = 30 m into Eq. (18.5), we obtain
k =\frac{E I}{L^{3}}\left[\begin{array}{cccccc}\frac{A L^{2}}{I} & 0 & 0 & -\frac{A L^{2}}{I} & 0 & 0 \\0 & 12 & 6 L & 0 & -12 & 6 L \\0 & 6 L & 4 L^{2} & 0 & -6 L & 2 L^{2} \\-\frac{A L^{2}}{I} & 0 & 0 & \frac{A L^{2}}{I} & 0 & 0 \\0 & -12 & -6 L & 0 & 12 & -6 L \\0 & 6 L & 2 L^{2} & 0 & -6 L & 4 L^{2}\end{array}\right] (18.5)
 (1)
(1)
By using the fixed-end moment expressions given inside the back cover of the book, we evaluate the fixed-end moments due to the 2-kN/m load as
Q_{f 3} = -Q_{f 6} = \frac{2(30)^2}{12} = 150 kN-mBy applying equilibrium equations to the free body of the member, we obtain (Fig. 18.13(c))
Q_{f 2} = Q_{f 5} = 30 kNThus,
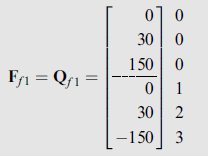 (2)
(2)
By using the structure degree of freedom numbers, 0, 0, 0, 1, 2, 3, for this member, the pertinent elements of K_1 and F_{f 1} are stored in their proper positions in the structure stiffness matrix S and the fixed-joint force vector P_f , respectively, as shown in Fig. 18.13(d).
Member 2 By substituting E = 201.4 kPa, I = 0.019 m^4, A = 833 cm², and L = 25 m into Eq. (18.5), we obtain
k_2 =\begin{bmatrix} 13,920 & 0 & 0 &-13,920 &0 &0 \\ 0 & 61.87 & 773.33 &0 &-61.87 &773.33\\ 0 & 773.33 & 12,888.89 &0 &-773.33 &6,444.44\\-13,920 & 0 & 0 & 13,920 & 0 & 0 \\ 0 & -61.87 & -773.33 & 0 & 61.87 & -773.33\\ 0 & 773.33 & 6,444.44 & 0 & -773.33 & 12,888.89 \end{bmatrix} (3)
Since member 2 is not subjected to any external loads,
Q_{f 2} = 0 (4)
By using the global coordinates of the beginning joint 3 and the end joint 2, we determine the direction cosines of member 2 as (Eq. (18.13))
\cos \theta=\frac{X_{e}-X_{b}}{L}=\frac{X_{e}-X_{b}}{\sqrt{\left(X_{e}-X_{b}\right)^{2}+\left(Y_{e}-Y_{b}\right)^{2}}} (18.13a)
\sin \theta=\frac{Y_{e}-Y_{b}}{L}=\frac{Y_{e}-Y_{b}}{\sqrt{\left(X_{e}-X_{b}\right)^{2}+\left(Y_{e}-Y_{b}\right)^{2}}} (18.13b)
\cos θ =\frac{X_2 – X_3}{L} = \frac{30 – 45}{25} = -0.6\sin θ =\frac{Y_2 – Y_3}{L} = \frac{0 – (-20)}{25} = 0.8
Substitution of these values into Eq. (18.12) yields the following transformation matrix for the member:
T =\left[\begin{array}{cccccc}\cos \theta & \sin \theta & 0 & 0 & 0 & 0 \\-\sin \theta & \cos \theta & 0 & 0 & 0 & 0 \\0 & 0 & 1 & 0 & 0 & 0 \\0 & 0 & 0 & \cos \theta & \sin \theta & 0 \\0 & 0 & 0 & -\sin \theta & \cos \theta & 0 \\0 & 0 & 0 & 0 & 0 & 1\end{array}\right] (18.12)
T_2 =\begin{bmatrix} -0.6 & 0.8 & 0 &0 &0 &0 \\ -0.8 & -0.6 & 0 &0 &0 &0\\ 0 & 0 & 1 &0 &0 &0\\0 & 0 & 0 & -0.6 & 0.8 & 0 \\ 0 & 0 & 0 & -0.8 & -0.6 & 0\\ 0 & 0 & 0 & 0 & 0 & 1 \end{bmatrix} (5)
To determine the member stiffness matrix in global coordinates, K_2, we substitute the matrices k_2 and T_2 into the relationship K = T^T kT (Eq. (18.26)) and carry out the necessary matrix multiplications to obtain
K = T^T kT (18.26)
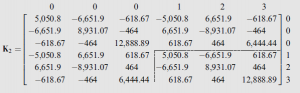 (6)
(6)
Note that K_2 is symmetric. By using the structure degree of freedom numbers, 0, 0, 0, 1, 2, 3, for member 2, the relevant elements of K_2 are added into their positions in the S matrix, as shown in Fig. 18.13(d). Note that F_{f 2} = 0.
Joint Load Vector By comparing Fig. 18.13(a) and (b), we write
P = \begin{bmatrix} 0 \\ 0\\75 \end{bmatrix}Joint Displacements The stiffness relations for the entire frame, P – P_f = Sd, are written in expanded form as
\begin{bmatrix} 0 \\ 0\\75 \end{bmatrix} – \begin{bmatrix} 0 \\ 30\\-150 \end{bmatrix} = \begin{bmatrix} 20,517.47 & -6,651.9 &618.67\\ -6,651.9 & 9,002.67 & -610.07\\618.67 & -610.07 &34,370.37 \end{bmatrix} \begin{bmatrix} d_1 \\ d_2\\d_3 \end{bmatrix}or
\begin{bmatrix} 0 \\ -30\\225 \end{bmatrix} = \begin{bmatrix} 20,517.47 & -6,651.9 &618.67\\ -6,651.9 & 9,002.67 & -610.07\\618.67 & -610.07 &34,370.37 \end{bmatrix} \begin{bmatrix} d_1 \\ d_2\\d_3 \end{bmatrix}By solving these equations simultaneously, we determine the joint displacements to be
d = \begin{bmatrix} -0.00149 m \\ -0.00399 m\\0.0065 rad \end{bmatrix}Member End Displacements and End Forces
Member 1
u_1 = v_1 = \begin{bmatrix} v_1 \\v_2\\v_3 \\ v_4 \\ v_5 \\ v_6 \end{bmatrix} \begin{matrix} 0 \\0\\0 \\ 1 \\ 2 \\ 3 \end{matrix} = \begin{bmatrix} 0 \\0\\0 \\ d_1 \\ d_2 \\ d_3 \end{bmatrix} = \begin{bmatrix} 0 \\0\\0 \\ -0.00149 m \\ -0.00399 m \\ 0.0065 rad \end{bmatrix}By substituting k_1,Q_{f 1}, and u1 in the member stiffness relationship Q = ku + Q_f (Eq. (18.4)), we determine the member end forces to be
Q = ku + Q_f (18.4)
F_1 = Q_1 =\left[\begin{array}{c}23.05 kN \\37.27 kN \\224.1 kN – m \\ -23.05 kN \\22.73 kN \\-6.08 kN – m\end{array}\right]Member 2
v_2 = \begin{bmatrix} v_1 \\v_2\\v_3 \\ v_4 \\ v_5 \\ v_6 \end{bmatrix} \begin{matrix} 0 \\0\\0 \\ 1 \\ 2 \\ 3 \end{matrix} = \begin{bmatrix} 0 \\0\\0 \\ d_1 \\ d_2 \\ d_3 \end{bmatrix} = \begin{bmatrix} 0 \\0\\0 \\ -0.00149 m \\ -0.00399 m \\ 0.0065 rad \end{bmatrix}By substituting K_2, v_2, and F_{f 2} = 0 into the member stiffness relationship in global coordinates, F = Kv + F_f (Eq.(18.25)), we determine the member end forces in global coordinates to be
F _{2}=\left[\begin{array}{c}-23.04 kN \\22.71 kN \\39.12 kN – m \\23.04 kN \\-22.71 kN \\81 kN – m\end{array}\right]The member end forces in local coordinates can now be evaluated by substituting F_2 \text{ and } T_2 into the relationship Q = TF (Eq. (18.11)).
Q _{2}=\left[\begin{array}{c}31.99 kN \\4.81 kN \\39.12 kN – m \\-31.99 kN \\-4.81 kN \\81 kN – m\end{array}\right]The end forces in the local coordinates of the members are shown in Fig. 18.13(e).
Support Reactions Since support joints 1 and 3 are the beginning joints for members 1 and 2, respectively, the reaction vectors R_① and R_③ must be equal to the upper halves of F_1 and F_2, respectively.
R_① = \left[\begin{array}{c}23.05 kN \\37.27 kN \\224.1 kN – m\end{array}\right] , R_③=\left[\begin{array}{c}-23.04 kN \\22.71 kN \\19.12 kN – m\end{array}\right]
The support reactions are shown in Fig. 18.13(f ).
Equilibrium Check Applying the equations of equilibrium to the entire frame (Fig. 18.13(f )), we obtain
+\rightarrow \sum F_{X}=0 23.05 – 23.04 = 0.01 ≈ 0 Checks
+\uparrow \sum F_{Y}=0 37.27 – 2(30) + 22.71 = -0.02 ≈ 0 Checks
+\circlearrowleft \sum M_{①}=0 224.1 – 2(30)(15) + 75 – 23.04(20) + 22.71(45) + 39.12
= -0.63 ≈ 0 Checks



