Question 11.15: Determine the reactions at the supports for the prismatic be...
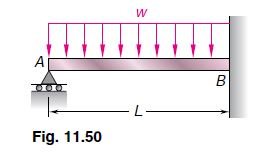
Determine the reactions at the supports for the prismatic beam and loading shown (Fig. 11.50).
The beam is statically indeterminate to the first degree. We consider the reaction at A as redundant and release the beam from that support. The reaction R _{A} is now considered as an unknown load (Fig. 11.51) and will be determined from the condition that the deflection y_{A} at A must be zero. By Castigliano’s theorem y_{A}=\partial U / \partial R_{A}, where U is the strain energy of the beam under the distributed load and the redundant reaction. Recalling Eq. (11.70), we write
x_{j}=\frac{\partial U}{\partial P_{j}}=\int_{0}^{L} \frac{M}{E I} \frac{\partial M}{\partial P_{j}} d x (11.70)
y_{A}=\frac{\partial U}{\partial R_{A}}=\int_{0}^{L} \frac{M}{E I} \frac{\partial M}{\partial R_{A}} d x (11.87)
We now express the bending moment M for the loading of Fig. 11.51.
The bending moment at a distance x from A is
M=R_{A} x-\frac{1}{2} w x^{2} (11.88)
and its derivative with respect to R_{A} is
\frac{\partial M}{\partial R_{A}}=x (11.89)
Substituting for M and \partial M / \partial R_{A} from (11.88) and (11.89) into (11.87), we write
y_{A}=\frac{1}{E I} \int_{0}^{L}\left(R_{A} x^{2}-\frac{1}{2} w x^{3}\right) d x=\frac{1}{E I}\left(\frac{R_{A} L^{3}}{3}-\frac{w L^{4}}{8}\right)
Setting y_{A}=0 and solving for R_{A}, we have
R_{A}=\frac{3}{8} w L R_{A}=\frac{3}{8} w L \uparrow
From the conditions of equilibrium for the beam, we find that the reaction at B consists of the following force and couple:
R _{B}=\frac{5}{8} w L \uparrow M_{B}=\frac{1}{8} w L^{2}\circlearrowright
