Question 15.CA.5: Determine the reactions at the supports for the prismatic be...
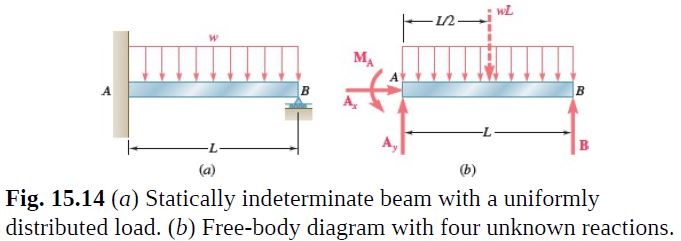
Determine the reactions at the supports for the prismatic beam of Fig. 15.14a.
Learn more on how we answer questions.
Equilibrium Equations. From the free-body diagram of Fig. 15.14b,
\begin{array}{lll}\stackrel{+}{\rightarrow} F_x=0: & & A_x=0 \\+\uparrow \Sigma F_y=0: & & A_y+B-w L=0 \\+\circlearrowleft \Sigma M_A=0: & & M_A+B L-\frac{1}{2} w L^2=0\end{array} (1)
Equation of Elastic Curve. Draw the free-body diagram of a portion of beam AC (Fig. 15.16) to obtain
+\circlearrowleft \Sigma M_C=0: \quad M+\frac{1}{2} w x^2+M_A-A_y x=0 (2)
Solving Eq. (2) for M and carrying into Eq. (15.4),
\frac{d^2 y}{d x^2}=\frac{M(x)}{E I} (15.4)
E I \frac{d^2 y}{d x^2}=-\frac{1}{2} w x^2+A_y x-M_AIntegrating in x gives
EI \theta=E I \frac{d y}{d x}=-\frac{1}{6} w x^3+\frac{1}{2} A_y x^2-M_A x+C_1 (3)
EI y=-\frac{1}{24} w x^4+\frac{1}{6} A_y x^3-\frac{1}{2} M_A x^2+C_1 x+C_2 (4)
Referring to the boundary conditions indicated in Fig. 15.15, we set x = 0, θ = 0 in Eq. (3); x = 0, y = 0 in Eq. (4); and conclude that C_1 = C_2 = 0. Thus, Eq. (4) is rewritten as
EI y=-\frac{1}{24} w x^4+\frac{1}{6} A_y x^3-\frac{1}{2} M_A x^2 (5)
But the third boundary condition requires that y = 0 for x = L. Carrying these values into Eq. (5),
0=-\frac{1}{24} w L^4+\frac{1}{6} A_y L^3-\frac{1}{2} M_A L^2or
3 M_A-A_y L+\frac{1}{4} w L^2=0 (6)
Solving this equation simultaneously with the three equilibrium equations of Eq. (1), the reactions at the supports are
A_x=0 \quad A_y=\frac{5}{8} w L \quad M_A=\frac{1}{8} w L^2 \quad B=\frac{3}{8} w L
