Question 18.3: Determine the shape factor of the T-section shown in Fig. 18...
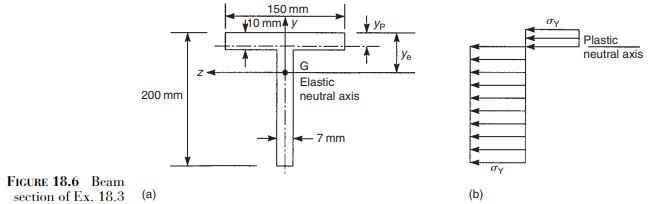
Determine the shape factor of the T-section shown in Fig. 18.6.
Learn more on how we answer questions.
In this case the elastic and plastic neutral axes are not coincident. Suppose that the former is a depth y_{\mathrm{e}} from the upper surface of the flange and the latter a depth y_{\mathrm{P}}. The elastic neutral axis passes through the centroid of the section, the location of which is found in the usual way. Hence, taking moments of areas about the upper surface of the flange
(150 \times 10+190 \times 7) y_{\mathrm{e}}=150 \times 10 \times 5+190 \times 7 \times 105
which gives
y_{\mathrm{e}}=52.0 \mathrm{~mm}
The second moment of area of the section about the elastic neutral axis is then, using Eq. (9.38)
I_{\mathrm{N}}={\frac{b d^{3}}{12}}+b d\left(-{\frac{d}{2}}\right)^{2}={\frac{b d^{3}}{3}} (9.38)
I=\frac{150 \times 52^{3}}{3}-\frac{143 \times 42^{3}}{3}+\frac{7 \times 148^{3}}{3}=11.1 \times 10^{6} \mathrm{~mm}^{4}
Therefore
Z_{\mathrm{e}}=\frac{11.1 \times 10^{6}}{148}=75000 \mathrm{~mm}^{3}
Note that we choose the least value for Z_{\mathrm{e}} since the stress will be a maximum at a point furthest from the elastic neutral axis.
The plastic neutral axis divides the section into equal areas (see Eq. (18.3)).
A_{1}=A_{2}={\frac{A}{2}} (18.3)
Inspection of Fig. 18.6 shows that the flange area is greater than the web area so that the plastic neutral axis must lie within the flange. Hence
150 y_{\mathrm{P}}=150\left(10-y_{\mathrm{P}}\right)+190 \times 7
from which
y_{\mathrm{P}}=9.4 \mathrm{~mm}
Equation (18.6)
Z_{\mathrm{P}}={\frac{A({{{\bar{y}_{1}}}}+{{{\bar{y}_{2}}}})}{2}} (18.6)
may be interpreted as the first moment, about the plastic neutral axis, of the area above the plastic neutral axis plus the first moment of the area below the plastic neutral axis. Hence
Z_{\mathrm{P}}=150 \times 9.4 \times 4.7+150 \times 0.6 \times 0.3+190 \times 7 \times 95.6=133800 \mathrm{~mm}^{3}
The shape factor f is, from Eq. (18.7)
f={\frac{M_{\mathrm{P}}}{M_{\mathrm{Y}}}}={\frac{\sigma _{\mathrm{Y}}Z_{\mathrm{P}}}{\sigma_{\mathrm{Y}}Z_{\mathrm{e}}}}={\frac{Z_{\mathrm{P}}}{Z_{\mathrm{e}}}} (18.7)
f=\frac{M_{\mathrm{P}}}{M_{\mathrm{Y}}}=\frac{Z_{\mathrm{P}}}{Z_{\mathrm{e}}}=\frac{133800}{75000}=1.78