Question 7.6: Discuss the eigenvibrations of a three-atom molecule. In the...
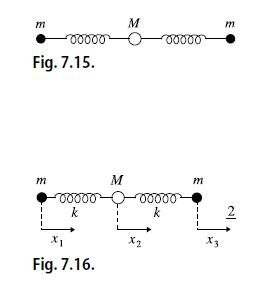
Discuss the eigenvibrations of a three-atom molecule. In the equilibrium state of the molecule, the two atoms of mass m are in the same distance from the atom of mass M. For simplicity one should consider only vibrations along the molecule axis connecting the three atoms, where the complicated interatomic potential is approximated by two strings (with spring constant k).
(a) Establish the equation of motion.
(b) Calculate the eigenfrequencies and discuss the eigenvibrations of the system.
(a) Let x_{1}, x_{2}, x_{3} be the displacements of the atoms from the equilibrium positions at time t . From Newton’s equations and Hooke’s law then it follows that
m\ddot{x}_{1} =−k(x_{1} −x_{2}),M\ddot{x}_{2} =−k(x_{2} −x_{3})− k(x_{2} − x_{1}) = k(x_{3} +x_{1} −2x_{2}),
m\ddot{x}_{3} =−k(x_{3}−x_{2}). (7.46)
(b) By inserting the ansatz x_{1} = a_{1} cos ωt, x_{2} = a_{2} cos ωt, and x_{3} = a_{3} cos ωt into (7.46), one obtains
(mω^{2} −k)a_{1} + ka_{2} = 0,ka_{1} + (Mω^{2} − 2k)a_{2} + ka_{3} = 0,
ka_{2} + (mω^{2} −k)a_{3} = 0. (7.47)
The eigenfrequencies of this system are obtained by setting the determinant of coefficients equal to zero:
\begin{vmatrix} mω^{2} −k & k & 0 \\ k & Mω^{2} − 2k & k \\ 0 &k & mω^{2} −k \end{vmatrix} =0 (7.48)
From this, it follows that
(mω^{2} − k)[ω^{4}mM −ω^{2}(kM +2km)] = 0 (7.49)
or
ω^{2}(mω^{2} −k)[ω^{2}mM −k(M +2m)] = 0.By factorization of (7.49) with respect to ω, one obtains for the eigenvibrations of the system:
ω_{1} = 0, ω_{2}=\sqrt{\frac{k}{m}}, ω_{3} =\sqrt{\frac{k}{m} \left(1 + \frac{2m}{M}\right)}.Discussion of the vibration modes:
(1) Insertion of ω = ω_{1} = 0 into (7.47) yields a_{1} = a_{2} = a_{3}. The eigenfrequency ω_{1} = 0 does not correspond to a vibrational motion, but represents only a uniform translation of the entire molecule: •→ ◦→ •→.
(2) Inserting ω = ω_{2} = (k/m)^{1/2} into (7.47) yields a_{1} =−a_{3}, a_{2} = 0; i.e., the central atom is at rest, while the outer atoms vibrate against each other: ←• ◦ •→.
(3) Inserting ω = ω_{3} = {k/m(1 + 2m/M)}^{1/2} into (7.47) yields a_{1} = a_{3}, a_{2} =−(2m/M)a_{1}, i.e., the two outer atoms vibrate in phase, while the central atom vibrates with opposite phase and with another amplitude: •→ ←◦ •→.
