Question 1.3.8: Evaluating and Simplifying a Difference Quotient If f(x) = 2...
Evaluating and Simplifying a Difference Quotient
If f(x) = 2x² – x + 3, find and simplify each expression:
a. f(x + h) b. \frac{f(x + h) – f(x)}{h}, h ≠ 0.
a. We find f(x + h) by replacing x with x + h each time that x appears in the equation.
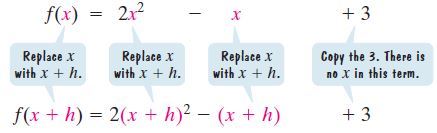
= 2(x² + 2xh + h²) – x – h + 3
= 2x² + 4xh + 2h² – x – h + 3
b. Using our result from part (a), we obtain the following:
=\frac{2x^2+4xh+2h^2-x-h+3-2x^2+x-3}{h} Remove parentheses and change the sign of each term in the parentheses.
Group like terms. Simplify.
=\frac{h(4x + 2h – 1)}{h} Factor h from the numerator.
= 4x + 2h – 1 Divide out identical factors of h in the numerator and denominator.