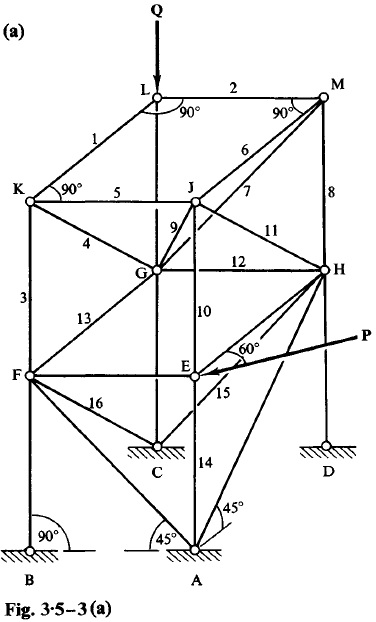
Question 3.5.3: Figure 3.5-3(a) shows a determinate space truss made up of h...
Figure 3.5-3(a) shows a determinate space truss made up of horizontal, vertical, and inclined members. The horizontal members and the vertical members are all of equal length. Member GJ is a diagonal of a cube, while all other inclined members are diagonals of equal squares. The truss is acted on by a vertical force Q at joint L; at joint E it is acted on by a horizontal force P which is inclined at 60° to member EH. Determine all member forces.
By Rule 1, member 1 is unstressed; similarly member 2 is unstressed.
By Rule 2 (with S_1 = 0), members 3, 4, and 5 are unstressed.
By Rule 2 (with S_2 =0), members 6, 7, and 8 are unstressed.
By Rule 2 (with S_5=S_6=0), members 9, 10, and 11 are unstressed.
At joint G, only the forces in four members (12, 13, LG, and GC) are unknown. Whence, by Rule 3, S_{12}= S_{13}= 0.
At joint E, with S_{10}known to be zero, then, for vertical equilibrium of the joint, member 14 must be unstressed.
At joint F, with S_{13}= 0, member 16 is the only one not lying in the plane of the others. Hence by Rule 1, member 16 is unstressed, i.e. S_{16}= 0.
By similar reasoning at joint H, member 15 is unstressed, i.e. S_{15}= 0.
With members 1 to 16 inclusive being unstressed, the only other members that might carry forces are as shown in Fig. 3.5-3(b).
By inspection,
