Question 8.15: Find and plot the radiation pattern of two parallel thin hal...
Find and plot the radiation pattern of two parallel thin half-wavelength electric dipoles separated by d = λ/2, λ, and 3λ/2. The mutual coupling of the dipoles is neglected.
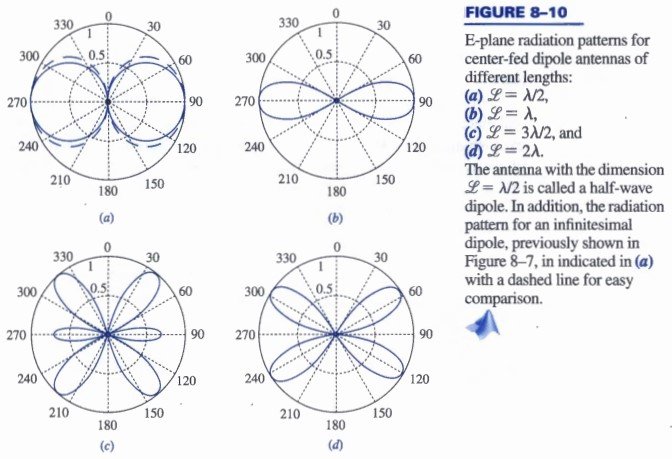
Here the radiation pattern of this linear array is calculated by applying the multiplication property (8.58), where the radiation pattern F_{1}(θ) of a single element (half-wavelength dipole with \mathscr{L} = λ/2) is given by (8.30) and presented by the first plot in Figure 8-10. The array factor for this case (in phase, excited with δ = 0) is obtained from (8.65) for N = 2, which yields F_{a}(θ) = \cos ( (kd/2) \cos θ) . The results for the total radiation pattern F(θ) for these three cases are plotted in the figures below for (a) d =λ/2, (b) d = λ, and (c) d = 3λ/2.
F(\theta ) \equiv F_{1}(\theta ) F_{a}(\theta ) = \left[\sin \theta \right] \times \left[\frac{\cos\left\lgroup\frac{k \mathscr{L}}{2} \cos\theta \right\rgroup – \cos\left\lgroup\frac{k \mathscr{L}}{2} \right\rgroup }{\sin^{2} \theta } \right] \\ \\ =\frac{\cos\left\lgroup\frac{k \mathscr{L}}{2} \cos\theta \right\rgroup – \cos\left\lgroup\frac{k \mathscr{L}}{2} \right\rgroup }{\sin \theta } (8.30)
F(\theta ,\phi ) = F_{1}(\theta ,\phi ) F_{a}(\theta ,\phi ) (8.58)
F_{a}(\theta ) = \frac{ \sin\left\lgroup\frac{N\psi }{2} \right\rgroup }{N \sin\left\lgroup \frac{\psi }{2} \right\rgroup } (8.65)
