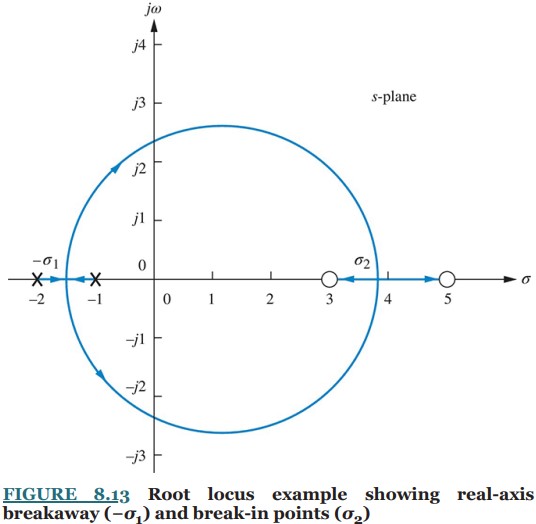
Question 8.3: Find the breakaway and break-in points for the root locus of...

Using the open-loop poles and zeros, we represent the open-loop system whose root locus is shown in Figure 8.13 as follows:

KG (s) H (s) = \frac{K (s  −  3) (s  −  5)}{(s  +  1) (s  +  2)} = \frac{K (s²  −  8s  +  15)}{(s²  +  3s  +  2)}                   (8.33)

But for all points along the root locus, KG(s)H(s) = − 1, and along the real axis, s = σ. Hence,

\frac{K  (σ²  −  8σ  +  15)}{(σ²  +  3σ  +  2)} = -1                  (8.34)

Solving for K, we find

K = \frac{- (σ²  +  3σ  +  2)}{(σ²  –  8σ  +  15)}                         (8.35)

Differentiating K with respect to σ and setting the derivative equal to zero yields

\frac{dK}{dσ} = \frac{ (11σ²  –  26σ  –  61)}{(σ²  –  8σ  +  15)²} = 0                     (8.36)

Solving for σ, we find σ = − 1.45 and 3.82, which are the breakaway and break-in points.