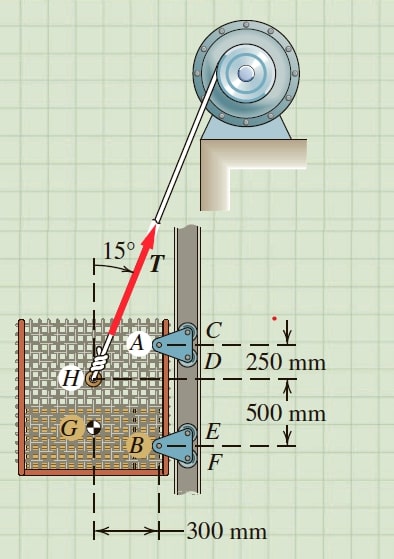
Question 1.7.1: Find the forces at A and B that act on the hopper shown on t...
Find the forces at A and B that act on the hopper shown on the left. Combined mass of hopper and its contents is 4000 kg and its center of mass, location where cable is applied and its orientation angle relative to the vertical (15°).This is a planar system. A and B are rollers in a vertical track.
Goal Find the forces at A and B that act on the hopper shown on the left.
Given Combined mass of hopper and its contents is 4000 kg and its center of mass, location where cable is applied and its orientation angle relative to the vertical (15°).
Assume This is a planar system. A and B are rollers in a vertical track. Hopper is in equilibrium.
Draw Free body diagram of hopper.
Formulate Equations Based on equilibrium conditions (Newton’s first law) and the free-body diagram, we write:
\sum{F_{x} } =T \sin 15^{\circ } + F_{Ax} +F_{Bx}=0 (A)
\sum{F_{y} } =T \sin 15^{\circ } – W=0 (B)
where W = (4000 kg)(9.8 m/s² ) = 39.2 kN
With moment center at H, we write:
\sum{M_{z @ H} } =(- F_{Ax}) (0.25 m)+(F_{Bx})(0.5 m) =0 (C)
Solve
From (B), T cos 15° = 39.2 kN ⇒ T = 40.58 kN (D)
From (C), F_{Ax} =2 F_{Bx} (E)
Substitute (D) and (E) into (A):
40.58 kN(\sin 15^{\circ }) +2 F_{Bx} + F_{Bx} = 0 \Rightarrow F_{Bx} = – 3.50 kN
Substitute this into (E) to find:
F_{Ax}= – 7.00 kN
or in vector notation,
\vec{F}_{B x} = – 3.50 kN\vec{i} ; F_{Ax}= – 7.00 kN \vec{i}
Answers \vec{F}_{B } = – 3.50 kN\vec{i}
\qquad \qquad \vec{F}_{A} = – 7.00 kN \vec{i}
Check It makes sense that A bears more of the load than B since it is closer to the point of application of the force.
