Question 12.3: Find the kinetic energy of a homogeneous circular top (densi...
Find the kinetic energy of a homogeneous circular top (density \varrho, mass m, height h, vertex angle 2α),
(a) rolling on a plane, and
(b) whose base circle rolls on a plane while its longitudinal axis is parallel to the plane and the vertex is fixed at a point.
Learn more on how we answer questions.
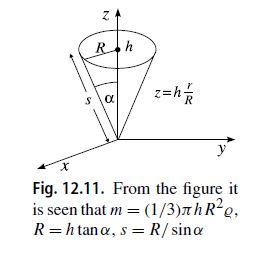
For the calculation of the tensor of inertia, we choose the coordinate system so that the longitudinal axis coincides with the z-axis.
Obviously,
Θ_{xx} =\varrho \int\limits_{V}{(y^{2} +z^{2})dV} = \varrho \iiint{(r^{2} sin^{2} \varphi +z^{2})r dz dr d\varphi}=\varrho \int\limits_{0}^{2π}{d\varphi} \int\limits_{0}^{R}{r dr} \int\limits_{h(r/R)}^{h}{(r^{2} sin^{2} \varphi +z^{2})dz}
=\varrho \frac{π}{20} hR^{2}(R^{2} +4h^{2}),
Θ_{xx} = \frac{3}{20} mh^{2}(tan^{2} α +4). (12.37)
For reasons of symmetry, we have
Θ_{yy} = Θ_{xx}.
Likewise,
Θ_{zz} =\varrho \int_{V}{(x^{2} +y^{2})dV} = \varrho \iiint{r^{3} dz dr d\varphi}=\varrho \int\limits_{0}^{2π}{d\varphi} \int\limits_{0}^{R}{r^{3} dr} \int\limits_{h(r/R)}^{h}{dz}= \frac{π}{10} \varrho hR^{4},
Θ_{zz} = \frac{3}{10} mh^{2} tan^{2} α. (12.38)
Since the integrals over \varphi of xy = r^{2} cos \varphi sin \varphi, xz = rz cos \varphi, yz = rz sin \varphi with the limits 0 and 2π vanish, follows Θ_{xy} = Θ_{xz} = Θ_{yz} = 0. The adopted system is a system of principal axes. We therefore set Θ_{1} = Θ_{xx} = Θ_{2},Θ_{3} = Θ_{zz}.
(a) The kinetic energy in the representation of principal axes reads
T = \frac{1}{2} Θ_{1}ω^{2}_{1} + \frac{1}{2} Θ_{2}ω^{2}_{2}+ \frac{1}{2} Θ_{3}ω^{2}_{3}. (12.39)
Since we already know the principal axes of inertia and moments of inertia, it remains only to express the motion of the cone by the corresponding angular velocities. The momentary rotation of the cone happens with the angular velocity ω about a line of support.We can express ω by \dot{\varphi} by considering the velocity of the point B. On the one hand v_{B} = \dot{\varphi} h cos α, and on the other hand v_{B} = ω · R cos α. From this, we find
ω= \dot{\varphi} \frac{h}{R}. (12.40)
\varphi is the polar angle of the figure axis (or, equivalently, the tangential line) in the x^{′} ,y^{′} – plane; \dot{\varphi} is the corresponding angular velocity.
A decomposition of ω in the system of principal axes, where ω lies in the x,z-plane, leads to ω_{2} = 0 and
ω_{3} = ω cos α and ω_{1} = sin α. (12.41)
For the kinetic energy, we thus obtain from (12.39)
T = \frac{1}{2} Θ_{1}ω^{2}_{1} + \frac{1}{2} Θ_{2}ω^{2}_{2}+ \frac{1}{2} Θ_{3}ω^{2}_{3}= \frac{1}{2} \frac{3}{20} mh^{2}(tan^{2} α + 4)ω^{2}_{1} + \frac{1}{2} \frac{3}{10} mh^{2} tan^{2} α^{2}
= \frac{3}{40} mh^{2}ω^{2} sin^{2} α(tan^{2} α +4)+ \frac{3}{20} mh^{2}ω^{2} sin^{2} α
= \frac{3}{40} mh^{2}ω^{2} \left(\frac{sin^{4} α}{cos^{2} α}+6 sin^{2} α\right). (12.42)
If we replace ω by (12.40) and employ R/h = tan α = sin α/ cos α, then
T = \frac{3}{40} mh^{2} \dot{\varphi}^{2} \frac{h^{2}}{R^{2}} \left(\frac{R^{2}}{h^{2}} sin^{2} α +6 cos^{2} α \frac{R^{2}}{h^{2}} \right)= \frac{3}{40} mh^{2} \dot{\varphi}^{2}(1 +5 cos^{2} α). (12.43)
(b) The momentary rotation axis ω is again the connecting line between the fixed vertex and the point of support. The relation between ω and \dot{\varphi} is likewise obtained by considering the velocity of point A.
We have v_{A} = h · \dot{\varphi} = ωR cos α, from which it follows that ω= \dot{\varphi} /sin α. The projection of ω onto the principal axes yields
ω_{1} = ω sin α = \dot{\varphi} ,
ω_{2} = 0, (12.44)
ω_{3} = ω cos α =\dot{\varphi} \frac{h}{R}.
Hence, for the kinetic energy, it follows from (12.39) that
T = \frac{1}{2} \frac{3}{20} mh^{2}(tan^{2} α +4)ω^{2}_{1}+ \frac{1}{2} \frac{3}{10} mh^{2} tan^{2} α ω^{2}_{3}
= \frac{3}{40} mh^{2} \dot{\varphi}^{2} \left( \frac{R^{2}}{h^{2}} +4+ 2 \frac{R^{2}}{h^{2}} · \frac{h^{2}}{R^{2}} \right)= \frac{3}{40} mh^{2} \dot{\varphi}^{2} \left(6 +\frac{R^{2}}{h^{2}}\right). (12.45)