Question 16.4: FINDING THE ELECTRIC POTENTIAL GOAL Calculate the electric p...
FINDING THE ELECTRIC POTENTIAL
GOAL Calculate the electric potential due to a collection of point charges.
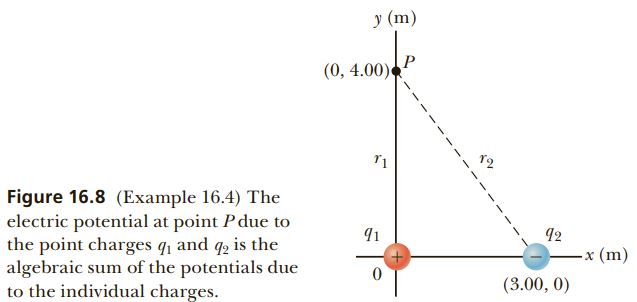
PROBLEM A 5.00-\mu \mathrm{C} point charge is at the origin, and a point charge q_{2}=-2.00 \mu \mathrm{C} is on the x-axis at (3.00, 0) \mathrm{m}, as in Figure 16.8. (a) If the electric potential is taken to be zero at infinity, find the electric potential due to these charges at point P with coordinates (0, 4.00) \mathrm{m}. (b) How much work is required to bring a third point charge of 4.00 \mu \mathrm{C} from infinity to P ?
STRATEGY For part (a), the electric potential at P due to each charge can be calculated from V=k_{e} q / r. The electric potential at P is the sum of these two quantities. For part (b), use the work-energy theorem, together with Equation 16.5,
PE = k_e \frac{q_1 q_2}{r} [16.5]
recalling that the potential at infinity is taken to bero.
Learn more on how we answer questions.
(a) Find the electric potential at point P.
Calculate the electric potential at P due to the 5.00-\mu \mathrm{C} charge:
\begin{aligned}V_{1} &=k_{e} \frac{q_{1}}{r_{1}}=\left(8.99 \times 10^{9} \frac{\mathrm{N} \cdot \mathrm{m}^{2}}{\mathrm{C}^{2}}\right)\left(\frac{5.00 \times 10^{-6} \mathrm{C}}{4.00 \mathrm{~m}}\right) \\&=1.12 \times 10^{4} \mathrm{~V}\end{aligned}
Find the electric potential at P due to the -2.00-\mu \mathrm{C} charge:
\begin{aligned}V_{2} &=k_{e} \frac{q_{2}}{r_{2}}=\left(8.99 \times 10^{9} \frac{\mathrm{N} \cdot \mathrm{m}^{2}}{\mathrm{C}^{2}}\right)\left(\frac{-2.00 \times 10^{-6} \mathrm{C}}{5.00 \mathrm{~m}}\right) \\&=-0.360 \times 10^{4} \mathrm{~V}\end{aligned}
Sum the two quantities to find the total electric potential at P:
\begin{aligned}V_{P} &=V_{1}+V_{2}=1.12 \times 10^{4} \mathrm{~V}+\left(-0.360 \times 10^{4} \mathrm{~V}\right) \\&=7.60 \times 10^{3} \mathrm{~V}\end{aligned}
(b) Find the work needed to bring the 4.00-\mu \mathrm{C} charge from infinity to P.
Apply the work-energy theorem, with Equation 16.5:
\begin{aligned} W=&\Delta P E=q_{3} \Delta V=q_{3}\left(V_{P}-V_{\infty}\right) \\ =&\left(4.00 \times 10^{-6} \mathrm{C}\right)\left(7.60 \times 10^{3} \mathrm{~V}-0\right) \\ W=&3.04 \times 10^{-2} \mathrm{~J}\end{aligned}
REMARKS Unlike the electric field, where vector addition is required, the electric potential due to more than one charge can be found with ordinary addition of scalars. Further, notice that the work required to move the charge is equal to the change in electric potential energy. The sum of the work done moving the particle plus the work done by the electric field is zero ( W_{\text {other }}+ W_{\text {electric }}=0 ) because the particle starts and ends at rest. Therefore, W_{\text {other }}=-W_{\text {electric }}=\Delta U_{\text {electric }}=q \Delta V.