Question 0.1.22: Finding the Zeros of a Cubic Polynomial Find the zeros of ...

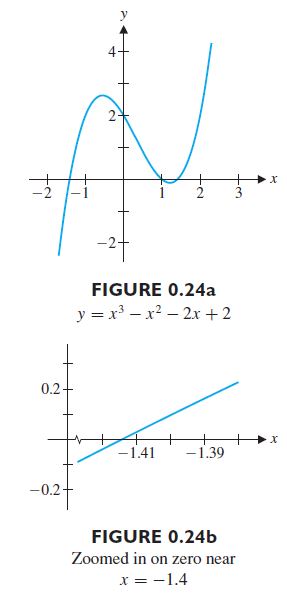
By calculating f (1), you can see that one zero of this function is x = 1, but how many other zeros are there? A graph of the function (see Figure 0.24a) shows that there are two other zeros of f , one near x = −1.5 and one near x = 1.5. You can find these zeros more precisely by using your graphing calculator or computer algebra system to zoom in on the locations of these zeros (as shown in Figures 0.24b and 0.24c). From these zoomed graphs it is clear that the two remaining zeros of f are near x = 1.41 and x = −1.41. You can make these estimates more precise by zooming in even more closely. Most graphing calculators and computer algebra systems can also find approximate zeros, using a built-in “solve” program. In Chapter 3, we present a versatile method (called Newton’s method) for obtaining accurate approximations to zeros. The only way to find the exact solutions is to factor the expression (using either long division or synthetic division). Here, we have

f(x)=x^3-x^2-2 x+2=(x-1)\left(x^2-2\right)=(x-1)(x-\sqrt{2})(x+\sqrt{2}),

from which you can see that the zeros are x=1, x=\sqrt{2} \text { and } x=-\sqrt{2} \text {. }