Question 11.S-P.6: For the beam and loading shown, determine the deflection at ...
For the beam and loading shown, determine the deflection at point D. Use E = 29 × 10^6 psi.

Learn more on how we answer questions.
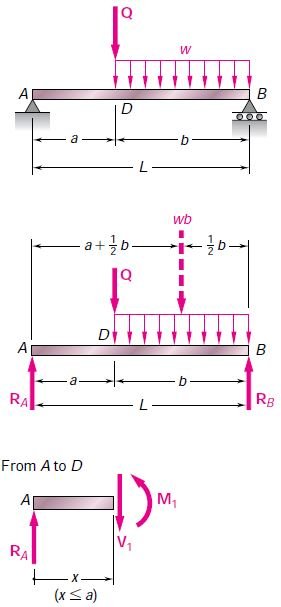
Castigliano’s Theorem. Since the given loading does not include a vertical load at point D, we introduce the dummy load Q as shown. Using Castigliano’s theorem and noting that EI is constant, we write
y_{D}=\int \frac{M}{E I}\left(\frac{\partial M}{\partial Q}\right) d x=\frac{1}{E I} \int M\left(\frac{\partial M}{\partial Q}\right) d x (1)
The integration will be performed separately for portions AD and DB.
Reactions. Using the free-body diagram of the entire beam, we find
R _{A}=\frac{w b^{2}}{2 L}+Q \frac{b}{L} \uparrow R _{B}=\frac{w b\left(a+\frac{1}{2} b\right)}{L}+Q \frac{a}{L} \uparrow
Portion AD of Beam. Using the free body shown, we find
M_{1}=R_{A} x=\left(\frac{w b^{2}}{2 L}+Q \frac{b}{L}\right) x \frac{\partial M_{1}}{\partial Q}=+\frac{b x}{L}
Substituting into Eq. (1) and integrating from A to D gives
\frac{1}{E I} \int M_{1} \frac{\partial M_{1}}{\partial Q} d x=\frac{1}{E I} \int_{0}^{a} R_{A} x\left(\frac{b x}{L}\right) d x=\frac{R_{A} a^{3} b}{3 E I L}We substitute for R_A and then set the dummy load Q equal to zero.
\frac{1}{E I} \int M_{1} \frac{\partial M_{1}}{\partial Q} d x=\frac{w a^{3} b^{3}}{6 E I L^{2}} (2)
Portion DB of Beam. Using the free body shown, we find that the bending moment at a distance v from end B is
M_{2}=R_{B} v-\frac{w v^{2}}{2}=\left[\frac{w b\left(a+\frac{1}{2} b\right)}{L}+Q \frac{a}{L}\right] v-\frac{w v^{2}}{2} \frac{\partial M_{2}}{\partial Q}=+\frac{a v}{L}
Substituting into Eq. (1) and integrating from point B where v = 0, to point D where v = b, we write
\frac{1}{E I} \int M_{2} \frac{\partial M_{2}}{\partial Q} d v=\frac{1}{E I} \int_{0}^{b}\left(R_{B} v-\frac{w v^{2}}{2}\right)\left(\frac{a v}{L}\right) d v=\frac{R_{B} a b^{3}}{3 E I L}-\frac{w a b^{4}}{8 E I L}Substituting for R_B and setting Q = 0,
\frac{1}{E I} \int M_{2} \frac{\partial M_{2}}{\partial Q} d v=\left[\frac{w b\left(a+\frac{1}{2} b\right)}{L}\right] \frac{a b^{3}}{3 E I L}-\frac{w a b^{4}}{8 E I L}=\frac{5 a^{2} b^{4}+a b^{5}}{24 E I L^{2}} w (3)
Deflection at Point D. Recalling Eqs. (1), (2), and (3), we have
y_{D}=\frac{w a b^{3}}{24 E I L^{2}}\left(4 a^{2}+5 a b+b^{2}\right)=\frac{w a b^{3}}{24 E I L^{2}}(4 a+b)(a+b)=\frac{w a b^{3}}{24 E I L}(4 a+b)From Appendix C we find that I=68.9 in ^{4} for a W10 × 15. Substituting for I, w, a, b, and L their numerical values, we obtain
y_{D}=0.262 in . \downarrow