Question 9.SP.7: For the section shown, the moments of inertia with respect t...

STRATEGY: The first step is to compute the product of inertia with respect to the x and y axes, treating the section as a composite area of three rectangles. Then you can use Eq. (9.25) to find the principal axes and Eq. (9.27) to find the principal moments of inertia.

\tan 2\theta _m = \frac{2I_{xy}}{I_x – I_y}              (9.25)

I_{\max , \ \min} = \frac{I_x + I_y}{2} \pm \sqrt{\left(\frac{I_x – I_y}{2}\right)^2 + I_{xy}^2}             (9.27)

MODELING and ANALYSIS: Divide the area into three rectangles as
shown (Fig. 1). Note that the product of inertia I_{x^{\prime} y^{\prime}}  with respect to centroidal axes parallel to the x and y axes is zero for each rectangle. Thus, using the parallel-axis theorem

I_{x y}=I_{x^{\prime} y^{\prime}}+\bar{x} \bar{y} A
you find that I_{x y} reduces to \bar{x} \bar{y} A for each rectangle.

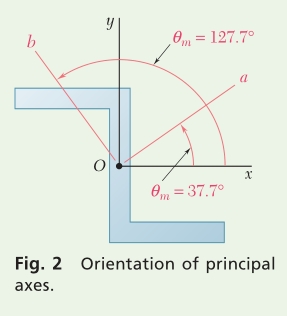
a. Principal Axes. Since you know the magnitudes of I_{x}, I_{y}, and I_{xy},you can use Eq. (9.25) to determine the values of θ_{m} (Fig. 2):

\begin{aligned}&\tan 2 \theta_{m}=-\frac{2 I_{x y}}{I_{x}-I_{y}}=-\frac{2(-6.56)}{10.38-6.97}=+3.85\\&2 \theta_{m}=75.4^{\circ} \text { and } 255.4^{\circ}\\&\theta_{m}=37.7^{\circ} \quad \text { and } \quad \theta_{m}=127.7^{\circ}\end{aligned}
b. Principal Moments of Inertia. Using Eq. (9.27), you have

REFLECT and THINK: Note that the elements of the area of the section are more closely distributed about the b axis than about the a axis. Therefore, you can conclude that I_{a}= I_{max}=15.45 in^{4} and I_{b} = I_{min} = 1.897 in^{4}. You can verify this conclusion by substituting θ = 37.7° into Eqs. (9.18) and (9.19).

I_{x^{\prime}}=\frac{I_{x}+I_{y}}{2}+\frac{I_{x}-I_{y}}{2} \cos 2 \theta-I_{x y} \sin 2 \theta               (9.18)

I_{y^{\prime}}=\frac{I_{x}+I_{y}}{2}-\frac{I_{x}-I_{y}}{2} \cos 2 \theta+I_{x y} \sin 2 \theta                (9.19)