Question A.01: For the triangular area of Fig. A.7, determine (a) the first...

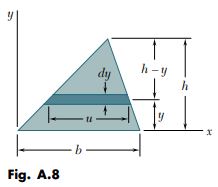
(a) First Moment Q_{x}. We select as an element of area a horizontal strip of length u and thickness d y, and note that all the points within the element are at the same distance y from the x axis (Fig. A.8). From similar triangles, we have

\frac{u}{b}=\frac{h-y}{h} \quad u=b \frac{h-y}{h}

and

d A=u d y=b \frac{h-y}{h} d y

The first moment of the area with respect to the x axis is

\begin{aligned} Q_{x} & =\int_{A} y d A=\int_{0}^{h} y b \frac{h-y}{h} d y=\frac{b}{h} \int_{0}^{h}\left(h y-y^{2}\right) d y \\ & =\frac{b}{h}\left[h \frac{y^{2}}{2}-\frac{y^{3}}{3}\right]_{0}^{h} \quad Q_{x}=\frac{1}{6} b h^{2} \end{aligned}

(b) Ordinate of Centroid. Recalling the first of Eqs. (A.4) and observing that A=\frac{1}{2} b h, we have

\begin{gathered} Q_{x}=A \bar{y} \quad \frac{1}{6} b h^{2}=\left(\frac{1}{2} b h\right) \bar{y} \\ \bar{y}=\frac{1}{3} h \end{gathered}