Question 8.1.3: Gaussian Elimination with Back-Substitution Use matrices to ...

Step 1 Write the augmented matrix for the system.

Step 2 Use matrix row operations to simplify the matrix to row-echelon form, with 1s down the main diagonal from upper left to lower right, and 0s below the 1s in the first and second columns. Our first step in achieving this goal is to get 1 in the top position of the first column.

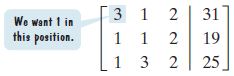
To get 1 in this position, we interchange row 1 and row 2: R_1↔R_2. (We could also interchange row 1 and row 3 to attain our goal.)

Now we want to get 0s below the 1 in the first column.

To get a 0 where there is now a 3, multiply the top row of numbers by -3 and add these products to the second row of numbers: -3R_1 + R_2. To get a 0 where there is now a 1, multiply the top row of numbers by -1 and add these products to the third row of numbers: -1R_1 + R_3. Although we are using row 1 to find the products, the numbers in row 1 do not change.

We move on to the second column. To get 1 in the desired position, we multiply -2 by its reciprocal, -\frac{1}{2}. Therefore, we multiply all the numbers in the second row by -\frac{1}{2}: -\frac{1}{2}R_2.

We are not yet done with the second column. The voice balloon shows that we want to get a 0 where there is now a 2. If we multiply the second row of numbers by -2 and add these products to the third row of numbers, we will get 0 in this position: -2R_2 + R_3. Although we are using the numbers in row 2 to find the products, the numbers in row 2 do not change.

We move on to the third column. To get 1 in the desired position, we multiply -4 by its reciprocal, -\frac{1}{4}. Therefore, we multiply all the numbers in the third row by -\frac{1}{4}: -\frac{1}{4}R_3.

We now have the desired matrix in row-echelon form, with 1s down the main diagonal and 0s below the 1s in the first and second columns.

Step 3 Write the system of linear equations corresponding to the matrix in step 2 and use back-substitution to find the system’s solution. The system represented by the matrix in step 2 is

We immediately see from equation (3) that the value for z is 5. To find y, we back-substitute 5 for z in the second equation.

y + 2z = 13                       Equation (2)

y + 2(5) = 13                   Substitute 5 for z.

y + 10 = 13                      Multiply.

y = 3                                 Subtract 10 from both sides and solve for y.

Finally, back-substitute 3 for y and 5 for z in the first equation.

x + y + 2z = 19             Equation (1)

x + 3 + 2(5) = 19         Substitute 3 for y and 5 for z.

x + 13 = 19                   Multiply and add.

x = 6                             Subtract 13 from both sides and solve for x.

With z = 5, y = 3, and x = 6, the solution set of the original system is {(6, 3, 5)}.
Check to see that the solution satisfies all three equations in the given system.