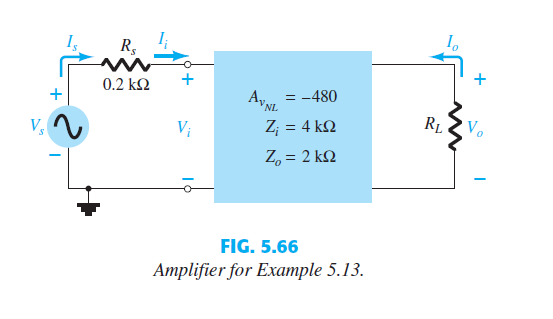
Question 5.13: Given the packaged (no-entry-possible) amplifier of Fig. 5.6...
Given the packaged (no-entry-possible) amplifier of Fig. 5.66 :
a. Determine the gain A_{v_{L}} and compare it to the no-load value with R_L = 1.2 kΩ .
b. Repeat part (a) with R_L = 5.6 kΩ and compare solutions.
c. Determine A_{v_{s}} with R_L = 1.2 kΩ .
d. Find the current gain A_{i}=\frac{I_{o}}{I_{i}}=\frac{I_{o}}{I_{s}} with R_L = 5.6 kΩ.
a. Eq. (5.89): A_{v_{L}}=\frac{R_{L}}{R_{L}+R_{o}} A_{v_{ NL }}
=\frac{1.2 k \Omega}{1.2 k \Omega+2 k \Omega}(-480)=(0.375)(-480)
= – 180
which is a dramatic drop from the no-load value.
b. Eq. (5.89): A_{v_{L}}=\frac{R_{L}}{R_{L}+R_{o}} A_{v_{ NL }}
=\frac{5.6 k \Omega}{5.6 k \Omega+2 k \Omega}(-480)=(0.737)(-480)
= – 353.76
which clearly reveals that the larger the load resistor, the better is the gain.
c. Eq. (5.96): A_{v_{s}}=\frac{R_{i}}{R_{i}+R_{s}} \cdot \frac{R_{L}}{R_{L}+R_{o}} A_{v_{ NL }}
=\frac{4 k \Omega}{4 k \Omega+0.2 k \Omega} \cdot \frac{1.2 k \Omega}{1.2 k \Omega+2 k \Omega}(-480)
= (0.952)(0.375)(-480)
= – 171.36
which is fairly close to the loaded gain A_v because the input impedance is considerably more than the source resistance. In other words, the source resistance is relatively small compared to the input impedance of the amplifier.
d. A_{i_{L}}=\frac{I_{o}}{I_{i}}=\frac{I_{o}}{I_{S}}=-A_{v_{L}} \frac{Z_{i}}{R_{L}}
=-(-353.76)\left(\frac{4 k \Omega}{5.6 k \Omega}\right)=-(-353.76)(0.714)
= 252.6