Question 1.3.5: Identifying Even or Odd Functions from Equations Determine w...
Identifying Even or Odd Functions from Equations
Determine whether each of the following functions is even, odd, or neither. Then determine whether the function’s graph is symmetric with respect to the y-axis, the origin, or neither.
a. f(x) = x³ – 6x b. g(x) = x^4 – 2x² c. h(x) = x² + 2x + 1
In each case, replace x with -x and simplify. If the right side of the equation stays the same, the function is even. If every term on the right side changes sign, the function is odd.
a. We use the given function’s equation, f(x) = x³ – 6x, to find f(-x).
There are two terms on the right side of the given equation, f(x) = x³ – 6x, and each term changed sign when we replaced x with -x. Because f(-x) = -f(x), f is an odd function. The graph of f is symmetric with respect to the origin.
b. We use the given function’s equation, g(x)=x^4-2 x^2, to find g(-x).
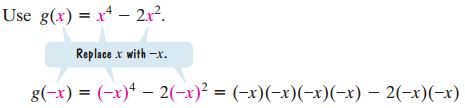
=x^4-2 x^2
The right side of the equation of the given function, g(x)=x^4-2 x^2, did not change when we replaced x with -x. Because g(-x) = g(x), g is an even function. The graph of g is symmetric with respect to the y-axis.
c. We use the given function’s equation, h(x) = x² + 2x + 1, to find h(–x).
The right side of the equation of the given function, h(x) = x² + 2x + 1, changed when we replaced x with -x. Thus, h(-x) ≠ h(x), so h is not an even function. The sign of each of the three terms in the equation for h(x) did not change when we replaced x with -x. Only the second term changed signs. Thus, h(-x) ≠ -h(x), so h is not an odd function. We conclude that h is neither an even nor an odd function. The graph of h is neither symmetric with respect to the y-axis nor with respect to the origin.