Question 4.13: Impact Analysis of a Diving Board A diving board, also refer...
Impact Analysis of a Diving Board
A diving board, also referred to as springboard, is a flexible board from which a dive may be executed, secured at one end and projecting over water at the other. Spring constant of a diving board is customarily adjusted by way of a fulcrum (roller support). Commercial fiberglass diving boards are made of molded fiberglass and a laminated Douglas fir wood core, with additional fiberglass that reinforces the tip and fulcrum area. Residential diving boards are usually fabricated of Douglas fir wood core with acrylic coating. Some springboards are made out of aluminum and there is frequently textured gripping material, such as crashed glass or sand mixed with the paint, to provide grip to persons not wearing shoes. It was shown in Example 2.3 using Ashby’s chart that glassreinforced plastic is one of the low-cost materials that make a beam (like diving board) as strong as possible for a given weight.
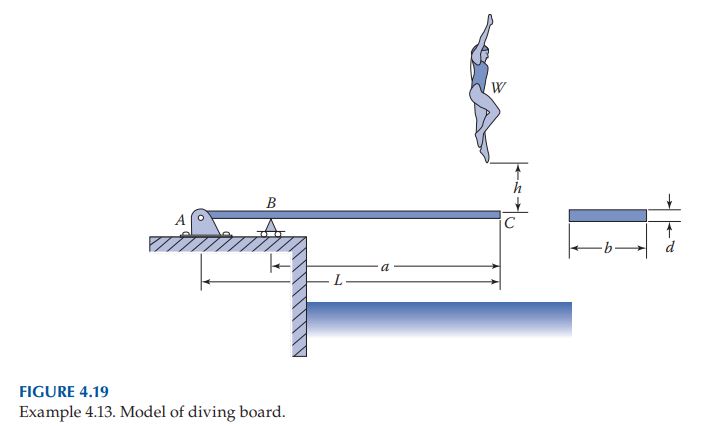
Given: A diver of weight W is springing on a rectangular cross-sectional diving board ABC (Figure 4.19). On a particular bounce, the diver reaches a height h above the end C of the board. Data are as follows:
a = 3 m L = 4 m b = 400 mm d = 65 mm
h = 500 mm E = 12.6 GPa W = 600 N
Find:
a. The maximum static deflection and stress in the board
b. The maximum dynamic deflection at end C
c. The maximum dynamic stress in the board
Assumptions:
1. The diver remains as a rigid mass when strikes the very end C of the board.
2. The flexural rigidity EI of the beam is constant.
3. The weight of the beam (e.g., fiberglass board) is much smaller than that of the diver and is neglected.
4. The deformation of the board due to the shear force is disregarded.
Learn more on how we answer questions.
The beam cross-sectional area properties are
\begin{array}{l} I=\frac{1}{12} b d^3=\frac{1}{12}(400)(65)^3=9.154\left(10^6\right) mm ^4 \\ c=\frac{1}{2}(65)=32.5 mm \end{array}
a. Static loading. The deflection at point C, from Case 10 of Table A.9, is
\upsilon _{s t}=\frac{W a^2 L}{3 E I} (c)
Introducing the given numerical values, we have
\upsilon _{s t}=\frac{600(3)^2(4)}{3\left(12.6 \times 10^9\right)(9.154)\left(10^{-6}\right)}=62.4 mm
The magnitude of the maximum moment M = Wa takes place at point B of the beam. The flexure formula results in therefore
\sigma_{s t}=\frac{M c}{I}=\frac{(600 \times 3)\left(32.5 \times 10^{-3}\right)}{9.154\left(10^{-6}\right)}=6.39 MPa
b. Maximum deflection at C. The impact factor, using Equation 4.32, is found to be
K=1+\sqrt{1+\frac{2 h}{\delta_{s t}}} (4.32)
K=1+\sqrt{1+\frac{2 h}{\upsilon _{s t}}}=1+\sqrt{1+\frac{2(500)}{62.4}}=5.126
Hence,
\upsilon _{\max }=K v _{s t}=5.126(62.4)=319.9 mm
c. Maximum stress in the board. Through the use of Equation 4.34, we have
\sigma_{\max }=K \sigma_{s t}=5.126(6.39)=32.8 MPa
which takes place at point B of the beam.
Comments: The results show that the dynamic deflection and dynamic stress in the diving board are much greater than the corresponding static quantities. But the actual values could be less than the calculated because of simplifying assumptions 3 and 4 of Section 4.7. A safety factor should be used to ensure against uncertainties related to strength of the board and the loading applied by the diver.