Question 15.SP.7: In the engine system shown, the crank AB has a constant cloc...
In the engine system shown, the crank AB has a constant clockwise angular velocity of 2000 rpm. For the crank position shown, determine (a) the angular velocity of the connecting rod BD, (b) the velocity of the piston P.
STRATEGY: Connecting rod BD is undergoing general motion, so use rigid-body kinematics. Crank AB is undergoing fixed axis rotation, and piston P is translating. The motion of the piston is the same as the end D of the connecting rod.

Learn more on how we answer questions.
MODELING and ANALYSIS:
Motion of Crank AB. The crank AB rotates about point A. Expressing \omega_{A B} in rad/s and writing v_B=r \omega_{A B}, you have (Fig. 1)
\begin{aligned}\omega_{A B} &=\left(2000 \frac{\mathrm{rev}}{\min }\right)\left(\frac{1 \mathrm{~min}}{60 \mathrm{~s}}\right)\left(\frac{2 \pi \mathrm{rad}}{1 \mathrm{rev}}\right)=209.4 \mathrm{rad} / \mathrm{s} \\v_B &=(A B) \omega_{A B}=(3 \mathrm{in} .)(209.4 \mathrm{rad} / \mathrm{s})=628.3 \mathrm{in} / \mathrm{s} \\\mathbf{v}_B &=628.3 \mathrm{in} . / \mathrm{s} \text{⦪}^{\circ} 50^{\circ}\end{aligned}
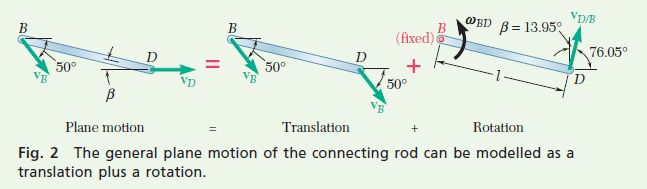
Motion of Connecting Rod BD. Consider this as a general plane motion. Using the law of sines, compute the angle β between the connecting rod and the horizontal as
\frac{\sin 40^{\circ}}{8 \text { in. }}=\frac{\sin \beta}{3 \text { in. }} \quad \beta=13.95^{\circ}
The velocity \mathrm{v}_D of point D where the rod is attached to the piston must be horizontal, while the velocity of point B is equal to the velocity \mathrm{v}_B obtained previously. Expressing the relation between the velocities \mathrm{v}_D, \mathrm{v}_B, and \mathrm{v}_{D/B}, you have
\mathbf{v}_D=\mathbf{v}_B + \mathbf{v}_{D / B}
This equation is shown pictorially in Fig. 2 where the motion of BD is resolved into a translation of B and a rotation about B.
Draw the vector diagram corresponding to this equation (Fig. 3). Recalling that β = 13.95°, you can determine the angles of the triangle and write
\frac{v_D}{\sin 53.95^{\circ}}=\frac{v_{D / B}}{\sin 50^{\circ}}=\frac{628.3 \mathrm{in} . / \mathrm{s}}{\sin 76.05^{\circ}}
\begin{aligned}v_{D / B} &=495.9 \mathrm{in} . / \mathrm{s} \quad \mathbf{v}_{D / B}=495.9 \mathrm{in} . / \mathrm{s} \text{⦨} 76.05^{\circ} \\v_D &=523.4 \mathrm{in} . / \mathrm{s}=43.6 \mathrm{ft} / \mathrm{s} \quad \mathbf{v}_D=43.6 \mathrm{ft} / \mathrm{s} \rightarrow\end{aligned}
\mathbf{v}_P=\mathbf{v}_D=43.6 \mathrm{ft} / \mathrm{s} \rightarrow
Since v_{D / B}=l \omega_{B D}, you have
495.9 \text { in./s }=(8 \text { in. }) \omega_{B D} \quad \omega_{B D}=62.0 \mathrm{rad} / \mathrm{s} \circlearrowleft
REFLECT and THINK: Note that as the crank continues to move clockwise below the center line, the piston changes direction and starts to move to the left. Can you see what happens to the motion of the connecting rod at that point? You can also solve this problem using the vector relationship expressed in Eq. (15.17′); this type of approach is shown in Sample Prob. 15.8.
\mathbf{v}_B=\mathbf{v}_A + \omega \mathbf{k} \times \mathbf{r}_{B / A} (15.17′)