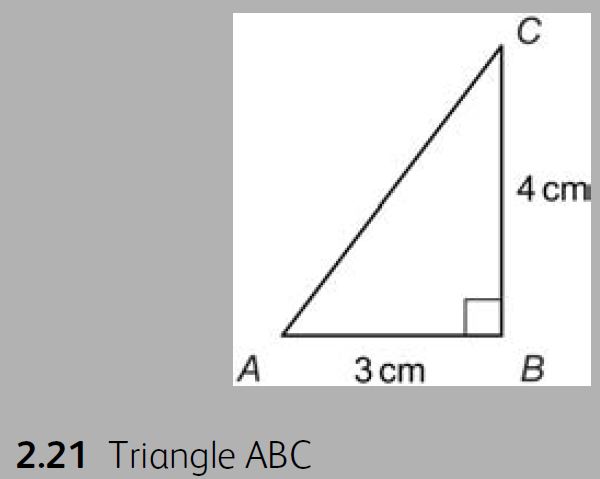
Question 2.41: In the triangle ABC shown in Figure 2.21, side AB = 3 cm and...
In the triangle ABC shown in Figure 2.21, side AB = 3 cm and side BC = 4 cm. Find the area of the triangle using both of the formulae given in Table 2.4.
| Shape | Area |
| Triangle | Half the base multiplied by the perpendicular height, or A=\frac{1}{2} \ b h |
| Triangle | A=\sqrt{s(s-a)(s-b)(s-c)} where a, b, c are the lengths of the sides and s=\frac{1}{2}(a+b+c) |
| Parallelogram | A = base multiplied by the perpendicular height between the parallel sides; the base can be any side of the parallelogram |
| Circle | A = πr² or A = \frac{\pi d^2}{4} where r = radius and d = diameter |
| Trapezium | Half the sum of the parallel sides (a, b) multiplied by the vertical distance (h) between them, or A = \left(\frac{a+b}{2}\right) \ h |
We can see from Figure 2.21 that this is a right-angled triangle, so the area A is found simply by using the formula A=\frac{1}{2} \ b h, where the base can be taken as either side containing the rectangle, then A=\frac{1}{2}(3)(4)=6 \ cm ^2. Note that the other side, not used as the base, is at right-angles to the base and is therefore the perpendicular height. If the triangle was not right angled, we would need to find the perpendicular height of all of the sides in order to find the area.
In our second formula, involving the sides of the triangle, we need to know side AC. Since this is a right-angled triangle, we can find the third side (opposite the right-angle) by using Pythagoras’ theorem. This states that the sum of the square of the hypotenuse is equal to the sum of the squares of the other two sides. In our case, we have: (AC)² = 3² + 4² = 9 + 16 = 25 or A C=\sqrt{25}=5. We now have three sides and s=\frac{1}{2}(a+b+c)=\frac{1}{2}(3+4+5)=6, so the area of the triangle is A=\sqrt{s(s-a)(s-b)(s-c)} =\sqrt{6(6-3)(6-4)(6-5)}=\sqrt{6(3)(2)(1)}= \sqrt{36}=6 \ cm ^2 as before.
We will now demonstrate the use of the parallelogram formula with another example.