Question 8.12: Kicking a soccer ball Now let’s consider the impulse associa...
Kicking a soccer ball
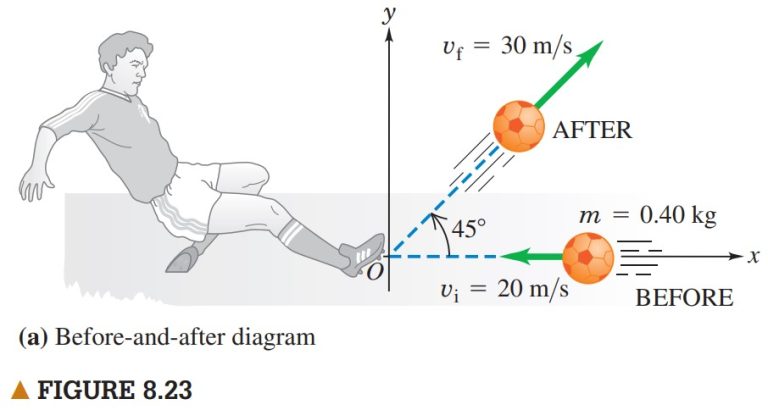
Now let’s consider the impulse associated with kicking a soccer ball (Figure 8.23a). The ball has mass 0.40 kg. Initially it moves horizontally to the left at 20 m/s, but then it is kicked and given a velocity with magnitude 30 m/s and direction 45° upward and to the right. Find the impulse of the force and the average force on the ball, assuming a collision time ∆t = 0.010 s.
Learn more on how we answer questions.
SET UP The velocities aren’t along the same line, so we must treat momentum and impulse as vector quantities, using their x and y components. As shown in Figure 8.23a, we point the x axis to the right and the y axis upward. We find the following initial and final velocity components:
\upsilon _{i,x}=-20 m/s, \upsilon _{i,y}=0,
\upsilon _{f,x} = \upsilon _{f,y}=\cos 45° (\upsilon _f)=(0.707)(30 m/s)=21 m/s.
SOLVE The x component of the impulse is equal to the x component of the change in momentum, and the same is true for the y components:
J_x =m(\upsilon _{f,x}-\upsilon _{i,x})= (0.40 kg)[21 m/s-(-20 m/s)]
= 16.4 kg · m/s,
J_y=m(\upsilon _{f,y}-\upsilon _{i,y})=(0.40 kg)(21 m/s – 0)=8.4 kg \cdot m/s
The components of average force on the ball (Figure 8.23b) are
F_{\mathrm{av},x}=\frac{J_x}{\Delta t}=1640 N, F_{\mathrm{av},y}=\frac{J_y}{\Delta t} = 840 N.
The magnitude and direction of the average force are, respectively,
F_{\mathrm{av}}=\sqrt{(1640 N)^2+ (840 N)^2}=1.8 \times 10^3 N,
\theta =\tan^{-1}\frac{840 N}{1640 N} = 27°,
where θ is measured counterclockwise from the +x axis.
REFLECT The direction of the ball’s final velocity is not the same as that of the average force acting on it. Indeed, there’s no reason it should be.
The average magnitude of force on the ball is about 400 lb; that’s roughly three times as much force as if you had just stood on the ball!
Practice Problem: Suppose the ball is moving at 30° downward from the horizontal before it is kicked. If all the numerical values are the same as before, find the magnitude and direction of the average force on the ball. Answers: 2.0 \times 10^3 N, 39°.
