Question 8.27: Let C be a circle in the z plane having its center on the re...
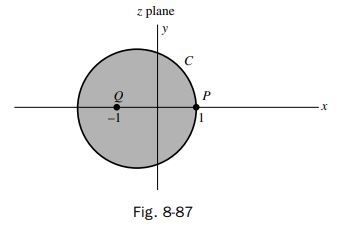
Let C be a circle in the z plane having its center on the real axis, and suppose further that it passes through z=1 and has z=-1 as an interior point. [See Fig. 8-87.] Determine the image of C in the w plane under the transformation w=f(z)=\frac{1}{2}(z+1 / z).
We have d w / d z=\frac{1}{2}\left(1-1 / z^{2}\right). Since d w / d z=0 at z=1, it follows that z=1 is a critical point. From the Taylor series of f(z)=\frac{1}{2}(z+1 / z) about z=1, we have
w-1=\frac{1}{2}\left[(z-1)^{2}-(z-1)^{3}+(z-1)^{4}-\cdots\right]
By Problem 8.100, we see that angles with vertices at z=1 are doubled under the transformation. In particular, since the angle at z=1 exterior to C is \pi, the angle at w=1 exterior to the image C^{\prime} is 2 \pi. Hence, C^{\prime} has a sharp tail at w=1 (see Fig. 8-88). Other points of C^{\prime} can be found directly.
It is of interest to note that in this case, C encloses the circle |z|=1, which under the transformation is mapped into the slit from w=-1 to w=1. Thus, as C approaches |z|=1, C^{\prime} approaches the straight line joining w=-1 to w=1.
