Question 30.5: One step in the manufacture of microelectronic devices is mi...
One step in the manufacture of microelectronic devices is microlithography, which traces a microscopic-circuit pattern on the silicon wafer. In one typical process, a thin polymer film, typically less than a thickness 2 μm, is coated over the surface of the silicon wafer. A microscopic template, called a mask, is placed over the surface, and irradiated. Radiation that passes through the very tiny holes in the mask hits the photoresist. For a negative photoresist, the radiation initiates reactions that greatly increase the molecular weight of polymer, rendering the photoresist insoluble in an organic solvent. The unreacted photoresist is then dissolved away from the silicon wafer with an organic solvent, and the circuit pattern is revealed by the reacted, insoluble photoresist.
Learn more on how we answer questions.
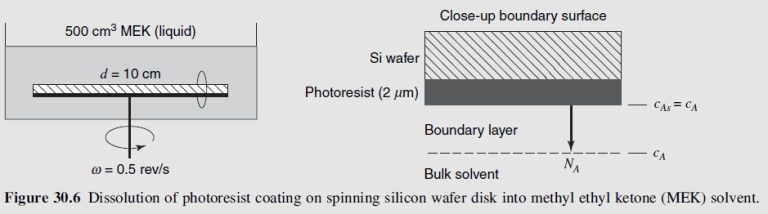
We are interested in using a ‘‘spinning disk’’ mass-transfer device shown in Figure 30.6 to study the photoresist-dissolution process within a closed tank of organic solvent. Consider a limiting case where all of the photoresist on surface of the wafer is soluble in the organic solvent. The negative photoresist is polystyrene (species A), and the organic solvent is methyl ethyl ketone (MEK, species B). The initial thickness of the photoresist coating \left(l_o\right) is 2 μm, the diameter of the wafer (d) is 10 cm, and the volume of the solvent in the tank (V) is 500 cm³. If the dissolution process is controlled by the convective mass-transfer rate at the polymer-solvent interface, determine the time required to completely dissolve the photoresist if the disk rotates at 0.5 rev/s (30 rpm). The solubility limit of the developed photoresist in the solvent \left(c_A^*\right) \text { is } 0.04 \mathrm{~g} / \mathrm{cm}^3 \text {, } and diffusivity of the photoresist in the solvent at infinite dilution \left(D_{A B}\right) \text { is } 2.93 \times 10^{-7} \mathrm{~cm}^2 / \mathrm{s} at a molecular weight of 7 \times 10^5 \mathrm{~g} / \mathrm{mol}, as reported by Tu and \text { Ouano. }^{26} The viscosity of the solvent (μ) is 5 \times 10^{-3} \mathrm{~g} / \mathrm{cm} \cdot \mathrm{s}, the density of the solvent (ρ) is 0.805 g/cm³, and the density of the solid polymer \left(\rho_A, \text { solid }\right) is 1.05 g/cm³. All physical properties are valid at the process temperature of 298 K. The mass-transfer correlation
for a spinning disk is given by
with
\operatorname{Re}=\frac{d^2 \omega}{\nu} (30-34)
where ω is the angular rotation rate (radians/time) of the disk.
The strategy for solving this problem is to develop a material-balance model for the process, and then incorporate the appropriate mass-transfer correlation(s) into the material-balance calculations.
The physical system represents a closed process where the polymer coating on the surface of the disk is the source for mass transfer, and the surrounding well-mixed organic solvent of constant volume is the sink for mass transfer. Under these assumptions, the unsteady-state material balance on the dissolved photoresist in the solvent phase of the well-mixed tank is
\left(\begin{array}{l} \text { rate of photoresist } \\ \text { added to solvent } \end{array}\right)+\left(\begin{array}{l} \text { rate of photoresist } \\ \text { exiting solvent tank } \end{array}\right)=\left(\begin{array}{l} \text { rate of accumulation of } \\ \text { photoresist within solvent } \end{array}\right)or
N_A \frac{\pi d^2}{4}-0=\frac{d\left(c_A V\right)}{d t}where \mathcal{c}_A represents the concentration of dissolved photoresist in the solvent at time t. The only input term is convective mass-transfer flux from the surface of the spinning disk \left(c_{A s}\right) to the solvent \left(c_A\right)
N_A=k_c\left(c_{A s}-c_A\right)At the polymer-solvent interface, the dissolved concentration of the photoresist is at its solubility limit. Furthermore, as the source is a pure component, c_A^*=c_{A s} remains constant. The material balance reduces to
k_c\left(c_{A s}-c_A\right) \frac{\pi d^2}{4}=V \frac{d c_A}{d t}Separation of the dependent variable c_A from the independent variable t, followed by integration from the initial condition, t=t_o, c_A=c_{A o}, to the final condition where all the photoresist is dissolved, t=t_f, c_A=c_{A f}, yields
-\int_{c_{A O}}^{c_{A f}} \frac{-d c_A}{c_{A s}-c_A}=\frac{k_c \pi d^2}{4 V} \int_{t_o}^{t_f} d tand finally
t_f-t_o=\frac{4 V}{\pi d^2 k_c} \ln \left(\frac{c_{A s}-c_{A o}}{c_{A s}-c_{A f}}\right)The final concentration c_{A f} and convective mass-transfer coefficient, k_c, must now be determined. First, c_{A f} is estimated by an overall material balance for the photoresist on the solid wafer and dissolved in the solution, i.e.,
c_{A f} V-c_{A o} V=m_{A o}-m_{A f}where m_A is the remaining mass of solid photoresist on the wafer, and m_{A o} is the initial mass, given by
m_{A o}=\rho_{A, \text { solid }} \frac{\pi d^2}{4} l_oWhen all the photoresist is dissolved, m_{A f}=0. If there is initially no photoresist dissolved in the solvent, then c_{A o}=0 and c_{A f} is
c_{A f}=\frac{m_{A o}}{V}=\frac{\rho_{A, \mathrm{solid}} \pi d^2 l_o}{4 V}=\frac{\left(1.05 \frac{\mathrm{g}}{\mathrm{cm}^2}\right) \pi(\mathrm{cm})^2\left(2.0 \mu \mathrm{m} \frac{1 \mathrm{~cm}}{10^4 \mu \mathrm{m}}\right)}{4 \cdot\left(500 \mathrm{~cm}^3\right)}=3.3 \times 10^{-5} \frac{\mathrm{g}}{\mathrm{cm}^3}The final concentration is well below the solubility limit of 0.04 g/cm³, and so all of the photoresist will dissolve. In order to calculate k_c, \mathrm{Sc} and Re are needed. For a dilute system, the fluid properties are essentially the properties of the solvent, and so Sc and Re are
\mathrm{Sc}=\frac{\mu}{\rho D_{A B}}=\frac{5 \times 10^{-5} \frac{\mathrm{g}}{\mathrm{cm} \cdot \mathrm{s}}}{\left(0.805 \frac{\mathrm{g}}{\mathrm{cm}^3}\right)\left(2.93 \times 10^{-7} \frac{\mathrm{cm}^2}{\mathrm{~s}}\right)}=21199\operatorname{Re}=\frac{d^2 \omega \rho}{\mu}=\frac{(10 \mathrm{~cm})^2\left(\frac{0.5 \mathrm{rev}}{\mathrm{s}} \frac{2 \pi \mathrm{rad}}{\mathrm{rev}}\right)\left(0.805 \frac{\mathrm{g}}{\mathrm{cm}^3}\right)}{5 \times 10^{-3} \frac{\mathrm{g}}{\mathrm{cm} \cdot \mathrm{s}}}=50,580
Consequently
\frac{k_c d}{D_{A B}}=0.62 \operatorname{Re}^{1 / 2} \mathrm{Sc}^{1 / 3}=0.62(50580)^{1 / 2}(21199)^{1 / 3}=3859or
k_c=\frac{3859 \cdot\left(2.93 \times 10^{-7} \frac{\mathrm{cm}^2}{\mathrm{~s}}\right)}{10 \mathrm{~cm}}=1.13 \times 10^{-4} \mathrm{~cm} / \mathrm{s}Finally, the time required to completely dissolve the photoresist is
t_f=\frac{(4)\left(500 \mathrm{~cm}^3\right)}{\pi(10 \mathrm{~cm})^2\left(1.13 \times 10^{-4} \frac{\mathrm{cm}}{\mathrm{s}}\right)} \ln \left(\frac{0.04-0}{0.04-3.3 \times 10^{-5}}\right)=46 \mathrm{~s}Notice that the concentration difference c_{A s}-c_A is relatively constant because c_A is very small. It is left to the reader to show that
W_A=k_c c_{A s} \frac{\pi d^2}{4}and
t_f=\frac{4 m_{A o}}{k_c c_{A s} \pi d^2}for the limiting case where c_{A s} \gg c_A, \text { i.e., } the surrounding solvent represents an infinite sink for mass transfer.