Question 17.7: Optimal Project Crashing Using the following information, de...
Optimal Project Crashing
Using the following information, develop the optimal time–cost solution. Project costs are $1,000 per day.
| Activity | Normal Time |
Crash Time |
Cost per Day to Crash |
| a | 6 | 6 | – |
| b | 10 | 8 | $500 |
| c | 5 | 4 | 300 |
| d | 4 | 1 | 700 |
| e | 9 | 7 | 600 |
| f | 2 | 1 | 800 |
Learn more on how we answer questions.
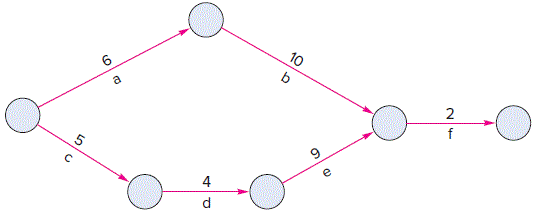
a. Determine which activities are on the critical path, its length, and the length of the other path:
| Path | Length |
| a–b–f | 18 |
| c–d–e–f | 20 (critical path) |
b. Rank the critical path activities in order of lowest crashing cost, and determine the number of days each can be crashed. Note: Available days = Normal time – Crash time
| Activity | Cost per Day to Crash | Available Days |
| c | $300 | 1 |
| e | 600 | 2 |
| d | 700 | 3 |
| f | 800 | 1 |
c. Begin shortening the project, one day at a time, and check after each reduction to see which path is critical. (After a certain point, another path may equal the length of the shortened critical path.) Thus:
(1) Shorten activity c one day at a cost of $300. The length of the critical path now becomes 19 days.
(2) Activity c cannot be shortened any more. Shorten activity e one day at a cost of $600. The length of path c–d–e–f now becomes 18 days, which is the same as the length of path a–b–f.
(3) The paths are now both critical; further improvements will necessitate shortening both paths.
The remaining activities for crashing and their costs are:
| Path | Activity | Crash cost per day |
| a–b–f | a | No reduction possible |
| b | $500 | |
| f | 800 | |
| c–d–e–f | c | No further reduction possible |
| d | $700 | |
| e | 600 | |
| f | 800 |
At first glance, it would seem that crashing f would not be advantageous, because it has the highest crashing cost. However, f is on both paths, so shortening f by one day would shorten both paths (and hence, the project) by one day for a cost of $800. The option of shortening the least expensive activity on each path would cost $500 for b and $600 for e, or $1,100. Thus, shorten f by one day. The project duration is now 17 days.
(4) At this point, no additional improvement is feasible. The cost to crash b is $500, and the cost to crash e is $600, for a total of $1,100. This would exceed the indirect project costs of $1,000 per day.
(5) The crashing sequence is summarized as follows:
| LENGTH AFTER CRASHING n DAYS | ||||
| Path | n=0 | 1 | 2 | 3 |
| a–b–f | 18 | 18 | 18 | 17 |
| c–d–e–f | 20 | 19 | 18 | 17 |
| Activity crashed | c | e | f | |
| Cost | $300 | $600 | $800 | |