Question 6.3.5: Rectangular-to-Polar Point Conversion Find polar coordinates...
Rectangular-to-Polar Point Conversion
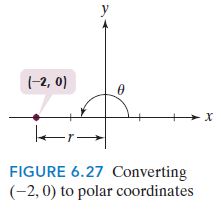
Find polar coordinates of the point whose rectangular coordinates are (-2, 0).
The blue check mark means that this solution has been answered and checked by an expert. This guarantees that the final answer is accurate.
Learn more on how we answer questions.
Learn more on how we answer questions.
We begin with (x, y) = (-2, 0) and find a set of polar coordinates (r, θ).
Step 1 Plot the point (x, y). The point (-2, 0) is plotted in Figure 6.27.
Step 2 Find r, the distance from the origin to (x, y). Can you tell by looking at Figure 6.27 that this distance is 2?
r=\sqrt{x^2+y^2}=\sqrt{(-2)^2+0^2}=\sqrt{4}=2.
Step 3 Find θ with θ lying on the same positive or negative axis as (x, y). The point (-2, 0) is on the negative x-axis. Thus, θ lies on the negative x-axis and θ = π. One representation of (-2, 0) in polar coordinates is (2, π).
Related Answered Questions
Question: 6.3.7
Verified Answer:
In each case, let’s express the rectangular equati...
Question: 6.3.6
Verified Answer:
Our goal is to obtain equations in which the varia...
Question: 6.3.2
Verified Answer:
a. We want r > 0 and 2π < θ < 4π. Using [...
Question: 6.3.4
Verified Answer:
We begin with (x, y) =(-1, \sqrt{3})[/latex...
Question: 6.3.3
Verified Answer:
We find (x, y) by substituting the given values fo...
Question: 6.3.1
Verified Answer:
a. To plot the point (r, θ) = (2, 135°), begin wit...