Question 16.2: Suppose that for the linear machine shown in Figure 16.6, we...
Suppose that for the linear machine shown in Figure 16.6, we have B = 1T, l = 0.3 m, V_T = 2 V, and R = 0.05 Ω. a. Assuming that the bar is stationary at t = 0, compute the initial current and the initial force on the bar. Also, determine the final (i.e., steady-state) speed assuming that no mechanical load is applied to the bar. b. Now, suppose that a mechanical load of 4 N directed to the left is applied to the moving bar. In steady state, determine the speed, the power delivered by V_T, the power delivered to the mechanical load, the power lost to heat in the resistance R_A, and the efficiency. c. Now, suppose that a mechanical pulling force of 2 N directed to the right is applied to the moving bar. In steady state, determine the speed, the power taken from the mechanical source, the power delivered to the battery, the power lost to heat in the resistance R_A, and the efficiency.

Learn more on how we answer questions.
a. Initially, for u = 0, we have e_A = 0, and the initial current is given by
i_A(0+) = \frac{V_T} {R_A} = \frac{2} {0.05} = 40 A
The resulting initial force on the bar is
f (0+) = Bli_A(0+) = 1(0.3)40 = 12 N
In steady state with no load, the induced voltage equals the battery voltage. Thus, we have
e_A = Blu = V_T
Solving for the velocity and substituting values, we get
u = \frac{V_T} {Bl} = \frac{2} {1(0.3)} = 6.667 m/s
b. Because the mechanical force opposes the motion of the bar, we have motor action. In steady state, the net force on the bar is zero—the force created by the magnetic field equals the load force. Thus, we obtain
f = Bli_A = f_{load}
Solving for the current and substituting values, we find that
i_A = \frac{f_{load}} {Bl} = \frac{4} {1(0.3)} = 13.33 A
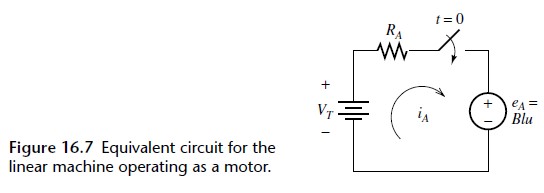
From the circuit shown in Figure 16.7, we have
e_A = V_T − R_Ai_A = 2 − 0.05(13.33) = 1.333 V
Now, we can find the steady-state speed:
u = \frac{e_A} {Bl} = \frac{1.333 }{1(0.3)} = 4.444 m/s
The mechanical power delivered to the load is
p_m = f_{load}u = 4(4.444) = 17.77 W
The power taken from the battery is
p_t = V_Ti_A = 2(13.33) = 26.67 W
The power dissipated in the resistance is
p_R = i^2_A R = (13.33)^2 × 0.05 = 8.889 W
As a check, we note that p_t = p_m + p_R to within rounding error. Finally, the efficiency of converting electrical power from the battery into mechanical power is
η = \frac{p_m}{ p_t} × 100\% = \frac{17.77}{ 26.67} × 100% = 66.67%
c. With a pulling force applied to the bar to the right, the bar speeds up, the induced voltage exceeds V_T, and current circulates counterclockwise, as illustrated in Figure 16.8. Thus, the machine operates as a generator. In steady state, the force induced by the field is directed to the left and equals the pulling force. Thus, we have
f = Bli_A = f_{pull}
Solving for i_A and substituting values, we find that
i_A = \frac{f_{pull}}{ Bl} = \frac{2}{ 1(0.3)} = 6.667 A
From the circuit shown in Figure 16.8, we obtain
e_A = V_T + R_Ai_A = 2 + 0.05(6.67) = 2.333 V
Now, we can find the steady-state speed:
u =\frac{ e_A} {Bl} = \frac{2.333} {1(0.3)} = 7.778 m/s
The mechanical power delivered by the pulling force is
p_m = f_{pull}u = 2(7.778) = 15.56 W
The power absorbed by the battery is
p_t = V_Ti_A = 2(6.667) = 13.33 W
The power dissipated in the resistance is
p_R = i^2_A R = (6.667)^2 × 0.05 = 2.222 W
As a check, we note that p_m = p_t + p_R to within rounding error. Finally, the efficiency of converting mechanical power into electrical power charging the battery is
η= \frac{p_t} {p_m} × 100\% = \frac{13.33} {15.56} × 100% = 85.67%