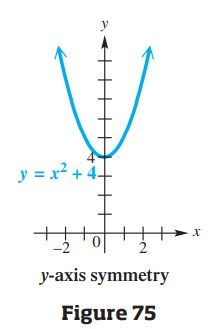Question 2.7.3: Testing for Symmetry with Respect to an Axis Test for symmet...
Testing for Symmetry with Respect to an Axis
Test for symmetry with respect to the x-axis and the y-axis.
(a) y = x² + 4 (b) x = y² – 3 (c) x² + y² = 16 (d) 2x + y = 4
(a) In y = x² + 4, replace x with -x.
\left.\begin{matrix} y= x ²+4\\ \\ y= (-x )²+4\\ \\ y= x ²+4 \end{matrix} \right\} \text{ The result is equivalent to the original equation.}
Thus the graph, shown in Figure 75, is symmetric with respect to the y-axis. The y-axis cuts the graph in half, with the halves being mirror images. Now replace y with -y to test for symmetry with respect to the x-axis.
\left.\begin{matrix} y= x ²+4\\ \\ -y=x²+4\\ \\ y= -x ²-4 \end{matrix} \right\} \text{ The result is not equivalent to the original equation.}
The graph is not symmetric with respect to the x-axis. See Figure 75.
(b) In x = y² – 3, replace y with -y.
x = (-y)² – 3 = y² – 3 Same as the original equation
The graph is symmetric with respect to the x-axis, as shown in Figure 76. It is not symmetric with respect to the y-axis.
(c) Substitute -x for x and then -y for y in x² + y² = 16.
(-x)² + y² = 16 and x² + (-y)²= 16
Both simplify to the original equation,
x² + y² = 16.
The graph, a circle of radius 4 centered at the origin, is symmetric with respect to both axes. See Figure 77.
(d) 2x + y = 4
Replace x with -x and then replace y with -y.
See Figure 78.
