Question 15.SP.23: The bent rod OAB rotates about the vertical axis OB. At the ...
The bent rod OAB rotates about the vertical axis OB. At the instant considered, its angular velocity and angular acceleration are, respectively, 20 rad/s and 200 rad/s², which are both clockwise when viewed from the positive Y axis. The collar D moves along the rod, and at the instant considered, OD = 8 in. The velocity and acceleration of the collar relative to the rod are, respectively, 50 in./s and 600 in./s², where both are upward. Determine (a) the velocity of the collar, (b) the acceleration of the collar.
STRATEGY: Use rigid-body kinematics with a rotating coordinate system since collar D is moving relative to the bent rod. Attach the rotating reference frame to the bent rod; then you can calculate its motion relative to the fixed frame and the collar’s motion relative to the rotating frame.
MODELING:
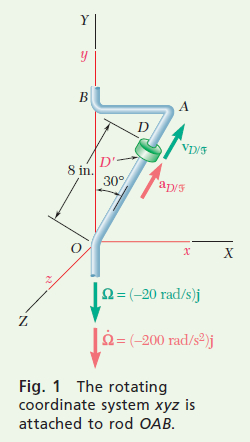
Frames of Reference. The angular velocity and angular acceleration of the bent rod (and rotating frame Oxyz) relative to the fixed frame OXYZ are \mathbf{\Omega}=(-20 \mathrm{rad} / \mathrm{s}) \mathbf{j} \text { and } \dot{\boldsymbol{\Omega}}=\left(-200 \mathrm{rad} / \mathrm{s}^2\right) \mathbf{j}, respectively (Fig. 1). The position vector of D is
\mathbf{r}=(8 \text { in. })\left(\sin 30^{\circ} \mathbf{i} + \cos 30^{\circ} \mathbf{j}\right)=(4 \text { in. }) \mathbf{i}+(6.93 \text { in. }) \mathbf{j}

Learn more on how we answer questions.
ANALYSIS:
a. Velocity \mathbf{v}_D. Denote the point of the rod that coincides with D by D^{\prime} and the rotating frame Oxyz by \mathscr{F} \text {. }. Then from Eq. (15.46) you have
\mathbf{v}_P=\mathbf{v}_{P^{\prime}} + \mathbf{v}_{P / \mathscr{F}} (15.46)
\mathbf{v}_D=\mathbf{v}_{D^{\prime}} + \mathbf{v}_{D / \mathscr{F}} (1)
where
\begin{aligned}\mathbf{v}_{D^{\prime}} &=\boldsymbol{\Omega} \times \mathbf{r}=(-20 \mathrm{rad} / \mathrm{s}) \mathbf{j} \times[(4 \mathrm{in} .) \mathbf{i} + (6.93 \mathrm{in} .) \mathbf{j}]=(80 \mathrm{in} . / \mathrm{s}) \mathbf{k} \\\mathbf{v}_{D / \mathscr{F}} &=(50 \mathrm{in} . / \mathrm{s})\left(\sin 30^{\circ} \mathbf{i} + \cos 30^{\circ} \mathbf{j}\right)=(25 \mathrm{in} . / \mathrm{s}) \mathbf{i} + (43.3 \mathrm{in} . / \mathrm{s}) \mathbf{j}\end{aligned}
Substituting the values obtained for \mathbf{V}_{D^{\prime}} and \mathbf{V}_{D / \mathscr{F}} into Eq. (1) gives
\mathbf{v}_D=(25 \text { in./s }) \mathbf{i} + (43.3 \text { in./s }) \mathbf{j}+(80 \text { in./s }) \mathbf{k}
b. Acceleration a_D. From Eq. (15.48), you have
\mathbf{a}_P=\mathbf{a}_{P^{\prime}} + \mathbf{a}_{P / \mathscr{F}} + \mathbf{a}_C (15.48)
\mathbf{a}_D=\mathbf{a}_{D^{\prime}} + \mathbf{a}_{D / \mathscr{F}} + \mathbf{a}_C (2)
where
\begin{aligned}\mathbf{a}_{D^{\prime}} &=\dot{\boldsymbol{\Omega}} \times \mathbf{r} + \boldsymbol{\Omega} \times(\boldsymbol{\Omega} \times \mathbf{r}) \\&=\left(-200 \mathrm{rad} / \mathrm{s}^2\right) \mathbf{j} \times[(4 \mathrm{in} .) \mathbf{i} + (6.93 \mathrm{in} .) \mathbf{j}] – (20 \mathrm{rad} / \mathrm{s}) \mathbf{j} \times(80 \mathrm{in} . / \mathrm{s}) \mathbf{k} \\&=+\left(800 \mathrm{in} . / \mathrm{s}^2\right) \mathbf{k} – \left(1600 \mathrm{in} . / \mathrm{s}^2\right) \mathbf{i} \\\mathbf{a}_{D / \mathscr{F}} &=\left(600 \mathrm{in} . / \mathrm{s}^2\right)\left(\sin 30^{\circ} \mathbf{i} + \cos 30^{\circ} \mathbf{j}\right)=\left(300 \mathrm{in} . / \mathrm{s}^2\right) \mathbf{i} + \left(520 \mathrm{in} . / \mathrm{s}^2\right) \mathbf{j} \\\mathbf{a}_C &=2 \boldsymbol{\Omega} \times \mathbf{v}_{D / \mathscr{F}} \\&=2(-20 \mathrm{rad} / \mathrm{s}) \mathbf{j} \times[(25 \mathrm{in} . / \mathrm{s}) \mathbf{i} + (43.3 \mathrm{in} . / \mathrm{s}) \mathbf{j}]=\left(1000 \mathrm{in} . / \mathrm{s}^2\right) \mathbf{k}\end{aligned}
Substituting the values obtained for \mathbf{a}_{D^{\prime}}, \mathbf{a}_{D / \mathscr{F}}, \text { and } \mathbf{a}_c into Eq. (2), you obtain
\mathbf{a}_D=-\left(1300 \text { in. } / \mathrm{s}^2\right) \mathbf{i} + \left(520 \mathrm{in} . / \mathrm{s}^2\right) \mathbf{j} + \left(1800 \mathrm{ in} . / \mathrm{s}^2\right) \mathbf{k}
REFLECT and THINK: For this problem, the 800 in./s² k in the \mathbf{a}_{D^{\prime}}, term corresponds to a tangential acceleration due to \dot{\boldsymbol{\Omega}}, while the -1600 in./s²i corresponds to a normal acceleration toward the axis of rotation. The Coriolis term reflects the fact that the \mathbf{v}_{D / \mathscr{F}} term is changing its direction due to Ω. When solving three-dimensional problems like this, the vector algebra approach is clearly superior to the method discussed in Sample Problem 15.20, since it is very difficult to visualize the direction of the acceleration terms.