Question 15.SP.13: The center of the double gear of Sample Prob. 15.6 has a vel...

MODELING and ANALYSIS:

a. Angular Acceleration of the Gear. In Sample Prob. 15.6, you found that  x_A=-r_1 \theta \text { and } v_A=-r_1 \omega.  Differentiating the second equation with respect to time, you obtain  a_A=-r_1 \alpha.

\begin{aligned}&v_A=-r_1 \omega           \quad 1.2  \mathrm{~m} / \mathrm{s}=-(0.150  \mathrm{~m}) \omega           \quad \omega=-8  \mathrm{rad} / \mathrm{s} \\&a_A=-r_1 \alpha           \quad 3  \mathrm{~m} / \mathrm{s}^2=-(0.150 \mathrm{~m}) \alpha \quad \alpha=-20  \mathrm{rad} / \mathrm{s}^2 \\&\end{aligned}

\alpha=\alpha \mathbf{k}=-\left(20  \mathrm{rad} / \mathrm{s}^2\right) \mathbf{k}

b. Accelerations. The relationship between the acceleration of any two points on a rigid body undergoing general plane motion is

\begin{aligned}\mathbf{a}_B &=\mathbf{a}_A  +  \mathbf{a}_{B / A}=\mathbf{a}_A  +  \left(\mathbf{a}_{B / A}\right)_t  +  \left(\mathbf{a}_{B / A}\right)_n \\&=\mathbf{a}_A  +  \alpha \mathbf{k} \times \mathbf{r}_{B / A}  –  \omega^2 \mathbf{r}_{B / A}\end{aligned}                   (1)

This equation indicates that the rolling motion of the gear can be thought of as a translation with A and a rotation about A (Fig. 1).

Acceleration of Point B. Substituting values into Eq. (1) gives

\begin{aligned}\mathbf{a}_B &=\mathbf{a}_A  +  \mathbf{a}_{B / A}=\mathbf{a}_A  +  \left(\mathbf{a}_{B / A}\right)_t  +  \left(\mathbf{a}_{B / A}\right)_n \\&=\mathbf{a}_A  +  \alpha \mathbf{k} \times \mathbf{r}_{B / A}  –  \omega^2 \mathbf{r}_{B / A} \\&=\left(3  \mathrm{~m} / \mathrm{s}^2\right) \mathbf{i}  –  \left(20  \mathrm{rad} / \mathrm{s}^2\right) \mathbf{k} \times(0.100  \mathrm{~m}) \mathbf{j}  –  (8  \mathrm{rad} / \mathrm{s})^2(0.100  \mathrm{~m}) \mathbf{j} \\&=\left(3  \mathrm{~m} / \mathrm{s}^2\right) \mathbf{i}  +  \left(2 \mathrm{~m} / \mathrm{s}^2\right) \mathbf{i}  –  \left(6.40  \mathrm{~m} / \mathrm{s}^2\right) \mathbf{j}\end{aligned}

\mathbf{a}_B=8.12 \mathrm{~m} / \mathrm{s}^2 \text { ⦪ } 52.0^{\circ}

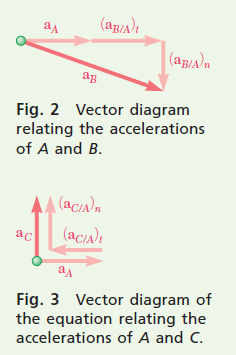
The vector triangle corresponding to this equation is shown in Fig. 2.

Acceleration of Point C Referring to Fig 3

\begin{aligned}\mathbf{a}_C &=\mathbf{a}_A  +  \mathbf{a}_{C / A}=\mathbf{a}_A  +  \alpha \mathbf{k} \times \mathbf{r}_{C / A}  –  \omega^2 \mathbf{r}_{C / A} \\&=\left(3  \mathrm{~m} / \mathrm{s}^2\right) \mathbf{i}  –  \left(20  \mathrm{rad} / \mathrm{s}^2\right) \mathbf{k} \times(-0.150  \mathrm{~m}) \mathbf{j}  –  (8  \mathrm{rad} / \mathrm{s})^2(-0.150  \mathrm{~m}) \mathbf{j} \\&=\left(3  \mathrm{~m} / \mathrm{s}^2\right) \mathbf{i}  – \left(3  \mathrm{~m} / \mathrm{s}^2\right) \mathbf{i}  +  \left(9.60  \mathrm{~m} / \mathrm{s}^2\right) \mathbf{j}\end{aligned}

\mathrm{a}_C=9.60  \mathrm{~m} / \mathrm{s}^2 \uparrow

Acceleration of Point D (Fig. 4).

\begin{aligned}\mathbf{a}_D &=\mathbf{a}_A  +  \mathbf{a}_{D / A}=\mathbf{a}_A  +  \alpha \mathbf{k} \times \mathbf{r}_{D / A}  –  \omega^2 \mathbf{r}_{D / A} \\&=\left(3  \mathrm{~m} / \mathrm{s}^2\right) \mathbf{i}  –  \left(20  \mathrm{rad} / \mathrm{s}^2\right) \mathbf{k} \times(-0.150  \mathrm{~m}) \mathbf{i}  –  (8  \mathrm{rad} / \mathrm{s})^2(-0.150  \mathrm{~m}) \mathbf{i} \\&=\left(3  \mathrm{~m} / \mathrm{s}^2\right) \mathbf{i}  +  \left(3  \mathrm{~m} / \mathrm{s}^2\right) \mathbf{j}  +  \left(9.60  \mathrm{~m} / \mathrm{s}^2\right) \mathbf{i}\end{aligned}

\mathbf{a}_D=12.95  \mathrm{~m} / \mathrm{s}^2 \text{⦨} 13.4^{\circ}

REFLECT and THINK: It is interesting to note that the x-component of acceleration for point C is zero since it is in direct contact with the fixed lower rack. It does, however, have a normal acceleration pointed upward. This is also true for a wheel rolling without slip.