Question 5.16: The composite beam shown in Fig. 5-47a is formed of a wood b...
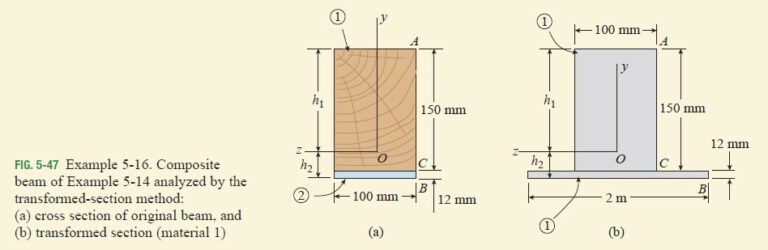
The composite beam shown in Fig. 5-47a is formed of a wood beam (100 mm × 150 mm actual dimensions) and a steel reinforcing plate (100 mm wide and 12 mm thick). The beam is subjected to a positive bending moment M=6 kN·m.
Using the transformed-section method, calculate the largest tensile and compressive stresses in the wood (material 1) and the maximum and minimum tensile stresses in the steel (material 2) if E_1 = 10.5 GPa and E_2 = 210 GPa.
Note: This same beam was analyzed previously in Example 5-14 above.
Learn more on how we answer questions.
Transformed section. We will transform the original beam into a beam of material 1, which means that the modular ratio is defined as
n=\frac{E_2}{E_1} =\frac{210 GPa}{10.5 GPa} = 20
The part of the beam made of wood (material 1) is not altered but the part made of steel (material 2) has its width multiplied by the modular ratio. Thus, the width of this part of the beam becomes
n(100 mm) = 20(100 mm) = 2 m
in the transformed section (Fig. 5-47b).
Neutral axis. Because the transformed beam consists of only one material, neutral axis passes through the centroid of the cross-sectional area. Therefore, with the top edge of the cross section serving as a reference line, and with the distance y_i measured positive downward, we can calculate the distance h_1 to the centroid as follows:
h_1=\frac{\sum{y_iA_i} }{\sum{A_i} } =\frac{(75 mm)(100 mm)(150 mm) +(156 mm)(2000 mm)(12 mm)}{(100 mm)(150 mm) + (2000 mm)(12 mm)}
=\frac{4869 \times 10^3 mm^3}{39 \times 10^3 mm^2} = 124.8 mm
Also, the distance h_2 from the lower edge of the section to the centroid is
h_2 = 162 mm – h_1 = 37.2 mm
Thus, the location of the neutral axis is determined.
Moment of inertia of the transformed section. Using the parallel-axis theorem (see Section 10.5 of Chapter 10, available online), we can calculate the moment of inertia I_T of the entire cross-sectional area with respect to the neutral axis as follows:
I_T=\frac{1}{12}(100 mm)(150 mm)^3+(100 mm)(150 mm)(h_1 – 75 mm)^2+\frac{1}{12} (2000 mm)(12 mm)^3+(2000 mm)(12 mm)(h_2 – 6 mm)^2
= 65.3\times 10^6 mm^4 + 23.7 \times 10^6 mm^4 = 89.0 \times 10^6 mm^4
Normal stresses in the wood (material 1). The stresses in the transformed beam (Fig. 5-47b) at the top of the cross section (A) and at the contact plane between the two parts (C) are the same as in the original beam (Fig. 5-47a). These stresses can be found from the flexure formula (Eq. 5-62), as follows:
\sigma _{x1}=-\frac{My}{I_T} (5-62)
\sigma _{1A}=-\frac{My}{I_T}=-\frac{(6 \times 10^6 N\cdot mm)(124.8 mm)}{89 \times 10^6 mm^4} = – 8.42 MPa
\sigma _{1C}=-\frac{My}{I_T} =-\frac{(6 \times 10^6 N\cdot mm)(-25.2 mm)}{89 \times 10^6 mm^4} = 1.13 MPa
These are the largest tensile and compressive stresses in the wood (material 1) in the original beam. The stress \sigma_{1A} is compressive and the stress \sigma_{1C} is tensile.
Normal stresses in the steel (material 2). The maximum and minimum stresses in the steel plate are found by multiplying the corresponding stresses in the transformed beam by the modular ratio n (Eq. 5-64). The maximum stress occurs at the lower edge of the cross section (B) and the minimum stress occurs at the contact plane (C):
\sigma _{x2}=-\frac{My}{I_T}n (5-64)
\sigma _{2B}=-\frac{My}{I_T}n=-\frac{(6 \times 10^6 N\cdot mm)(-37.2 mm)}{89 \times 10^6 mm^4}(20)= 50.2 MPa
\sigma _{2C}=-\frac{My}{I_T}n =-\frac{(6 \times 10^6 N\cdot mm)(-25.2 mm)}{89 \times 10^6 mm^4}(20)= 34 MPa
Both of these stresses are tensile.
Note that the stresses calculated by the transformed-section method agree with those found in Example 5-14 by direct application of the formulas for a composite beam