Question 2.4: THE DAYTONA 500 GOAL Apply the basic kinematic equations. PR...
THE DAYTONA 500
GOAL Apply the basic kinematic equations.
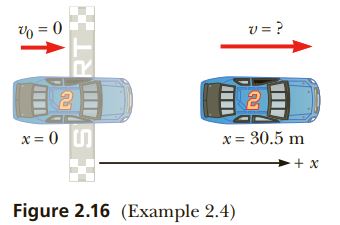
PROBLEM A race car starting from rest accelerates at a constant rate of 5.00 \mathrm{~m} / \mathrm{s}^{2}. (a) What is the velocity of the car after it has traveled 1.00 \times 10^{2} \mathrm{ft} ? (b) How much time has elapsed? (c) Calculate the average velocity two different ways.
STRATEGY We’ve read the problem, drawn the diagram in Figure 2.16, and chosen a coordinate system (steps 1 and 2). We’d like to find the velocity v after a certain known displacement \Delta x. The acceleration a is also known, as is the initial velocity v_{0} (step 3, labeling, is complete), so the third equation in Table 2.4 looks most useful for solving part (a). Given the velocity, the first equation in Table 2.4
| Table 2.4 equations for Motion in a straight Line Under Constant Acceleration | |
| Equation | Information Given by Equation |
| v = v_0 + at | Velocity as a function of time |
| \Delta_x = v_0 t + \frac{1}{2}at^2 | Displacement as a function of time |
| v^2 = v_0^2 + 2a\Delta x | Velocity as a function of displacement |
| Note: Motion is along the x– axis. At t = 0, the velocity of the particle is v_0. | |
can then be used to find the time in part (b). Part (c) requires substitution into Equations 2.2
\bar{v} ≡ \frac{Δx}{Δt} = \frac{x_f – x_i}{t_f – t_i} [2.2]
and 2.7,
\bar{v} ≡ \frac{v_0 + v}{2} (for constant α) [2.7]
respectively.
Learn more on how we answer questions.
(a) Convert units of \Delta x to SI, using the information in the inside front cover.
1.00 \times 10^{2} \mathrm{ft}=\left(1.00 \times 10^{2} \mathrm{ft}\right)\left(\frac{1 \mathrm{~m}}{3.28 \mathrm{ft}}\right)=30.5 \mathrm{~m}
Write the kinematics equation for v^{2}(step 4) :
v^{2} =v_{0}^{2}+2 a \Delta x
Solve for v, taking the positive square root because the car moves to the right (step 5):
v =\sqrt{v_{0}^{2}+2 a \Delta x}
Substitute v_{0}=0, a=5.00 \mathrm{~m} / \mathrm{s}^{2}, and \Delta x=30.5 \mathrm{~m} :
\begin{aligned}v &=\sqrt{v_{0}^{2}+2 a \Delta x}=\sqrt{(0)^{2}+2\left(5.00 \mathrm{~m} / \mathrm{s}^{2}\right)(30.5 \mathrm{~m})} \\&=17.5 \mathrm{~m} / \mathrm{s}\end{aligned}
(b) How much time has elapsed?
Apply the first equation of Table 2.4:
v=a t+v_{0}
Substitute values and solve for time t :
\begin{aligned}&17.5 \mathrm{~m} / \mathrm{s}=\left(5.00 \mathrm{~m} / \mathrm{s}^{2}\right) t \\&t=\frac{17.5 \mathrm{~m} / \mathrm{s}}{5.00 \mathrm{~m} / \mathrm{s}^{2}}=3.50 \mathrm{~s}\end{aligned}
(c) Calculate the average velocity in two different ways.
Apply the definition of average velocity, Equation 2.2:
\bar{v}=\frac{x_{f}-x_{i}}{t_{f}-t_{i}}=\frac{30.5 \mathrm{~m}}{3.50 \mathrm{~s}}=8.71 \mathrm{~m} / \mathrm{s}
Apply the definition of average velocity in Equation 2.7:
\bar{v}=\frac{v_{0}+v}{2}=\frac{0+17.5 \mathrm{~m} / \mathrm{s}}{2}=8.75 \mathrm{~m} / \mathrm{s}
REMARKS The answers are easy to check. An alternate technique is to use \Delta x=v_{0} t+\frac{1}{2} a t^{2} to find t and then use the equation v=v_{0}+a t to find v. Notice that the two different equations for calculating the average velocity, due to rounding, give slightly different answers.