Question 15.SP.19: The Geneva mechanism shown is used in many counting instrume...
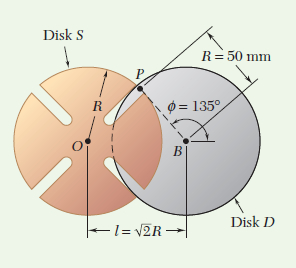
The Geneva mechanism shown is used in many counting instruments and in other applications where an intermittent rotary motion is required. Disk D rotates with a constant counterclockwise angular velocity of \boldsymbol{\omega}_D 10 rad/s. A pin P is attached to disk D and slides along one of several slots cut in disk \mathrm{S}. It is desirable that the angular velocity of disk \mathrm{S} be zero as the pin enters and leaves each slot; in the case of four slots, this occurs if the distance between the centers of the disks is l=\sqrt{2} R.
At the instant when \phi=150^{\circ}, determine (a) the angular velocity of disk \mathrm{S}, (b) the velocity of pin P relative to disk \mathrm{S}.
STRATEGY: You have two rigid bodies whose motions are related; therefore use rigid-body kinematics. Since point P is moving in a slot, use a rotating reference frame.
Learn more on how we answer questions.
MODELING and ANALYSIS:
Using geometry, you can solve triangle OPB, which corresponds to the position \phi = 150° (Fig. 1). Using the law of cosines, you have
r^2=R^2 + l^2 – 2 R l \cos 30^{\circ}=0.551 R^2 \quad r=0.742 R=37.1 \mathrm{~mm}
Then, from the law of sines, you have
\frac{\sin \beta}{R}=\frac{\sin 30^{\circ}}{r} \quad \sin \beta=\frac{\sin 30^{\circ}}{0.742} \quad \beta=42.4^{\circ}
Since pin P is attached to disk D and disk D rotates about point B, the magnitude of the absolute velocity of P is
\begin{aligned}v_P=R \omega_D=(50 \mathrm{~mm})(10 \mathrm{rad} / \mathrm{s}) &=500 \mathrm{~mm} / \mathrm{s} \\\mathbf{v}_P &=500 \mathrm{~mm} / \mathrm{s} \text { ⦫ } 60^{\circ}\end{aligned}
Now consider the motion of pin P along the slot in disk \mathrm{S}. Denote the point of disk \mathrm{S} that coincides with P by P′ at the instant considered and select a rotating frame \mathcal{S} attached to disk \mathrm{S}. Then from Eq. (15.33), you have
\mathbf{v}_P=\mathbf{v}_{P^{\prime}} + \mathbf{v}_{P / \mathcal{S}} (15.33)
\mathbf{v}_P=\mathbf{v}_{P^{\prime}} + \mathbf{v}_{P / \mathcal{S}} (1)
In Eq. (1), \mathbf{v}_{P^{\prime}} is perpendicular to the radius OP, and v_{P/\mathcal{S}} is directed along the slot. Draw the velocity triangle corresponding to Eq. (1) (see Fig. 2). From the triangle, you can compute
\begin{aligned}\gamma &=90^{\circ} – 42.4^{\circ} – 30^{\circ}=17.6^{\circ} \\v_{P^{\prime}} &=v_P \sin \gamma=(500 \mathrm{~mm} / \mathrm{s}) \sin 17.6^{\circ} \\\mathbf{v}_{P^{\prime}} &=151.2 \mathrm{~mm} / \mathrm{s} \text{ ⦮ } 42.4^{\circ} \\v_{P / \mathcal{S}} &=v_P \cos \gamma=(500 \mathrm{~mm} / \mathrm{s}) \cos 17.6^{\circ}\end{aligned}
\mathbf{v}_{P / \mathrm{S}}=\mathbf{v}_{P / \mathcal{S}}=477 \mathrm{~mm} / \mathrm{s} \text{⦫} 42.4^{\circ}
Since \mathbf{v}_{P^{\prime}} is perpendicular to the radius OP, you have
v_{P^{\prime}}=r \omega_{\mathcal{S}} \quad 151.2 \mathrm{~mm} / \mathrm{s}=(37.1 \mathrm{~mm}) \omega_{\mathcal{S}}
\omega_ \mathrm{S}=\omega_{\mathcal{S}}=4.08 \mathrm{rad} / \mathrm{s} \circlearrowright
REFLECT and THINK: The result of the Geneva mechanism is that disk \mathrm{S} rotates ¼ turn each time pin P engages, then it remains motionless while pin P rotates around before entering the next slot. Disk D rotates continuously, but disk S rotates intermittently. An alternative approach to drawing the vector triangle is to use vector algebra, as was done in Sample Prob. 15.18.

