Question 4.7: The magnitudes of normal stresses on two mutually perpendicu...
The magnitudes of normal stresses on two mutually perpendicular planes at a point in an elastic body are 60 MPa compressive and 80 MPa tensile. Find the magnitudes of shearing stresses on these planes, if the magnitude of one of the principal stresses is 100 MPa tensile. Find also the magnitude of the other principal stress at this point.
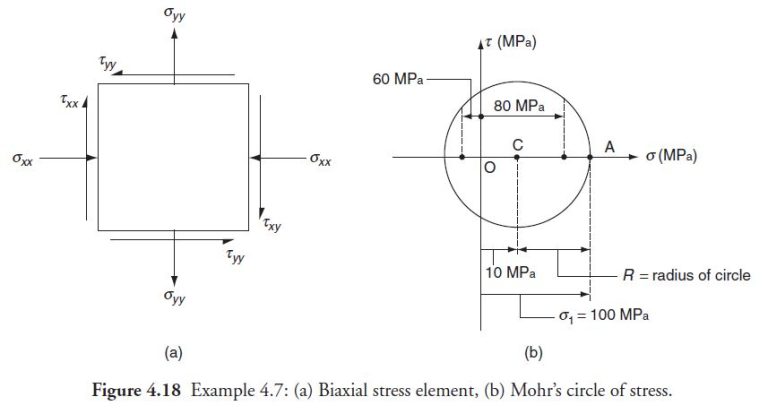
Let us show the stresses on a differential element with unknown shear stress assumed arbitrarily as shown in Figure 4.18(a). Also, we show the Mohr’s circle in the Figure 4.18(b). The circle is drawn by locating its centre,
C\left\lgroup \frac{\sigma_{x x}+\sigma_{y y}}{2}, 0 \right\rgroup
that is, (10, 0) MPa and the point (100, 0) MPa.
Clearly, the radius of the circle, R is
R = (100 -10) MPa = 90 MPa
Therefore,
(80-10)^2+\tau_{x y}^2=90^2 \Rightarrow \tau_{x y}^2=3200 \Rightarrow \tau_{x y}=\pm 56.57 MPa
Therefore, the magnitude of shear stress is
\tau_{x y}=\pm 56.57 MPa
If \sigma_2 be the other principal stress, then
\sigma_1+\sigma_2=\sigma_{x x}+\sigma_{y y}=-60+80=20
or \sigma_2=20-\sigma_1=20-100=-80
The other principal stress, \sigma_2=80 80 MPa (compressive).
