Question 10.2: The preliminary design of a motor-to-generator connection ca...
The preliminary design of a motor-to-generator connection calls for the use of a large hollow shaft with inner and outer diameters of 4 in. and 6 in., respectively. Knowing that the allowable shearing stress is 12 ksi, determine the maximum torque that can be transmitted by (a) the shaft as designed, (b) a solid shaft of the same weight, and (c) a hollow shaft of the same weight and an 8-in. outer diameter.

Learn more on how we answer questions.
STRATEGY: Use Eq. (10.9) to determine the maximum torque using the allowable stress.
\tau_{\text{max}}=\frac{T_c}{J} \quad \quad \quad \quad \pmb{(10.9)}
MODELING and ANALYSIS:
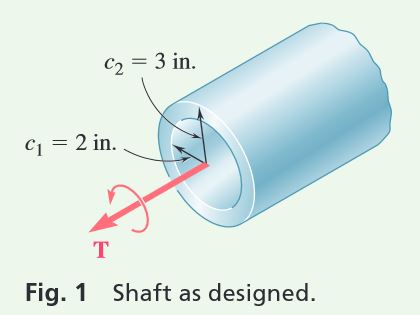
a. Hollow Shaft as Designed. Using Fig. 1 and setting \tau_{\text{all}}=12 \text{ ksi}, we write
J=\frac{\pi}{2}(c^4_2-c^4_1) =\frac{\pi}{2}[(3 \text{ in})^4-(2 \text{ in.})^4] =102.1 \text{ in}^4
Using Eq. (10.9), we write
\tau_{\text{max}}=\frac{Tc_2}{J} \quad \quad \quad 12 \text{ ksi}=\frac{T(3 \text{ in.})}{102.1 \text{ in}^4} \quad \quad T=408 \text{ kip.in.}
b. Solid Shaft of Equal Weight. For the shaft as designed and this solid shaft to have the same weight and length, their cross-sectional areas must be equal, i.e. A_{(a)}= A_{(b)}.
\pi[(3 \text{ in.})^2-(2 \text{ in.})^2]=\pi c^2_3 \quad \quad \quad c_3=2.24 \text{ in.}
Using Fig. 2 and setting \tau_{\text{all}}=12 \text{ ksi}, we write
\tau_{\text{max}}=\frac{Tc_3}{J} \quad \quad \quad 12 \text{ ksi}=\frac{T(2.24 \text{ in.})}{\frac{\pi}{2}(2.24 \text{ in.})^4 } \quad \quad \quad T=211 \text{ kip.in.}
c. Hollow Shaft of 8-in. Diameter. For equal weight, the cross-sectional areas again must be equal, i.e., A_{(a)}=A_{(c)} (Fig. 3). We determine the inside diameter of the shaft by writing
\pi[(3 \text{ in.})^2-(2 \text{ in.})^2]=\pi[(4 \text{ in.})^2-c^2_5] \quad \quad \quad c_5=3.317 \text{ in.}
For c_5=3.317 \text{ in.} \text{ and }c_4=4 \text{ in.,}
J=\frac{\pi}{2} [(4 \text{ in.})^4-(3.317 \text{ in.})^4] =212 \text{ in}^4
With \tau_{\text{all}}=12 \text{ ksi and }c_4=4 \text{ in.,}
\tau_{\text{max}}=\frac{Tc_4}{J} \quad \quad 12 \text{ ksi}=\frac{T(4 \text{ in.})}{212 \text{ in}^4} \quad \quad \quad T=636 \text{ kip.in.}
REFLECT and THINK: This example illustrates the advantage obtained when the shaft material is further from the centroidal axis.