Question 11.5: The Seesaw A father of mass mf and his daughter of mass md s...
The Seesaw
A father of mass m_f and his daughter of mass m_d sit on opposite ends of a seesaw at equal distances from the pivot at the center (Fig. 11.8). The seesaw is modeled as a rigid rod of mass M and length \ell and is pivoted without friction. At a given moment, the combination rotates in a vertical plane with an angular speed ω.
(A) Find an expression for the magnitude of the system’s angular momentum.
(B) Find an expression for the magnitude of the angular acceleration of the system when the seesaw makes an angle θ with the horizontal.

Learn more on how we answer questions.
(A) Conceptualize Identify the z axis through O as the axis of rotation in Figure 11.8. The rotating system has angular momentum about that axis.
Categorize Ignore any movement of arms or legs of the father and daughter and model them both as particles. The system is therefore modeled as a rigid object. This first part of the example is categorized as a substitution problem.
The moment of inertia of the system equals the sum of the moments of inertia of the three components: the seesaw and the two individuals. We can refer to Table 10.2 to obtain the expression for the moment of inertia of the rod and use the particle expression I = mr² for each person.
Find the total moment of inertia of the system about the z axis through O:
I=\frac{1}{12} M \ell^2+m_f\left(\frac{\ell}{2}\right)^2+m_d\left(\frac{\ell}{2}\right)^2=\frac{\ell^2}{4}\left(\frac{M}{3}+m_f+m_d\right)Find the magnitude of the angular momentum of the system:
L=I \omega=\frac{\ell^2}{4}\left(\frac{M}{3}+m_f+m_d\right) \omega(B) Conceptualize Generally, fathers are more massive than daughters, so the system is not in equilibrium and has an angular acceleration. We expect the angular acceleration to be positive in Figure 11.8.
Categorize The combination of the board, father, and daughter is a rigid object under a net torque because of the external torque associated with the gravitational forces on the father and daughter. We again identify the axis of rotation as the z axis in Figure 11.8.
Analyze To find the angular acceleration of the system at any angle θ, we first calculate the net torque on the system and then use \Sigma \tau_{\text {ext }}=I \alpha from the rigid object under a net torque model to obtain an expression for α.
Evaluate the torque due to the gravitational force on the father:
\tau_f=m_f g \frac{\ell}{2} \cos \theta \quad (\overrightarrow{\tau}_f out of page)
Evaluate the torque due to the gravitational force on the daughter:
\tau_d=-m_d g \frac{\ell}{2} \cos \theta \quad (\overrightarrow{\tau}_d into page)
Evaluate the net external torque exerted on the system:
\sum \tau_{\text{ext}}=\tau_f+\tau_d=\frac{1}{2}\left(m_f-m_d\right) g \ell \cos \thetaUse Equation 11.18 and I from part (A) to find α:
\sum \tau_{\text {ext }}=I \alpha (11.18)
\alpha=\frac{\sum \tau_{\text{ext}}}{I}=\frac{2\left(m_f-m_d\right) g \cos \theta}{\ell\left[(M / 3)+m_f+m_d\right]}Finalize For a father more massive than his daughter, the angular acceleration is positive as expected. If the seesaw begins in a horizontal orientation (θ = 0) and is released, the rotation is counterclockwise in Figure 11.8 and the father’s end of the seesaw drops, which is consistent with everyday experience.
| Table 10.2 Moments of Inertia of Homogeneous Rigid Objects with Different Geometries | ||
| Hoop or thin cylindrical shell I_{CM}= MR^2  |
Long, thin rod with rotation axis through center I_{CM}= \frac{1}{12}ML^2  |
Solid sphere I_{CM}= \frac{2}{5}MR^2 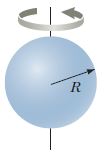 |
| Solid cylinder or disk I_{CM}= \frac{1}{2}MR^2  |
Long, thin rod with rotation axis through end I_{CM}= \frac{1}{3}ML^2  |
|
| Hollow cylinder I_{CM}= \frac{1}{2}M(R_1{}^2+R_2{}^2)  |
Rectangular plate I_{CM}= \frac{1}{12}M(a^2+b^2)  |
Thin spherical shell I_{CM}= \frac{2}{3}MR^2 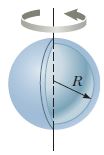 |