The uniform column AB consists of an 8-ft section of structural tubing having the cross

Question

The uniform column [latex]A B[/latex] consists of an 8 - [latex]\mathrm{ft}[/latex] section of structural tubing having the cross section shown. (a) Using Euler's formula and a factor of safety of two, determine the allowable centric load for the column and the corresponding normal stress. (b) Assuming that the allowable load, found in part [latex]a[/latex], is applied as shown at a point [latex]0.75 \mathrm{in}[/latex]. from the geometric axis of the column, determine the horizontal deflection of the top of the column and the maximum normal stress in the column. Use [latex]E=29 imes 10^{6}[/latex] psi.

Accepted Answer

Effective Length. Since the column has one end fixed and one end free, its effective length is

[latex]L_{e}=2(8 \mathrm{ft})=16 \mathrm{ft}=192 \mathrm{in}[/latex]

Critical Load. Using Euler's formula, we write

[latex]P_{ ext {cr }}=\frac{\pi^{2} E I}{L_{e}^{2}}=\frac{\pi^{2}\left(29 imes 10^{6} \mathrm{psi} ight)\left(8.00 \mathrm{in}^{4} ight)}{(192 \mathrm{in} .)^{2}} \quad P_{ ext {cr }}=62.1 \mathrm{kips}[/latex]

a. Allowable Load and Stress. For a factor of safety of 2, we find

[latex]P_{ ext {all }}=\frac{P_{ ext {cr }}}{F . S .}=\frac{62.1 \mathrm{kips}}{2} \quad P_{ ext {all }}=31.1 ext { kips }[/latex]

and

[latex]\sigma=\frac{P_{ ext {all }}}{A}=\frac{31.1 \mathrm{kips}}{3.54 \mathrm{in}^{2}} \quad \sigma=8.79 \mathrm{ksi}[/latex]

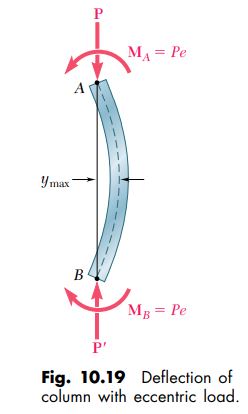
b. Eccentric Load. We observe that column [latex]A B[/latex] and its loading are identical to the upper half of the column of Fig. 10.19 which was used in the derivation of the secant formulas; we conclude that the formulas of Sec. 10.5 apply directly to the case considered here. Recalling that [latex]P_{ ext {all }} / P_{ ext {cr }}=\frac{1}{2}[/latex] and using Eq. (10.31), we compute the horizontal deflection of point A:

[latex] \begin{aligned} y_{m} & =e\left[\sec \left(\frac{\pi}{2} \sqrt{\frac{P}{P_{\mathrm{cr}}}} ight)-1 ight]=(0.75 \mathrm{in} .)\left[\sec \left(\frac{\pi}{2 \sqrt{2}} ight)-1 ight] \ & =(0.75 \mathrm{in} .)(2.252-1) \quad y_{m}=0.939 \mathrm{in.} \end{aligned} [/latex]

The maximum normal stress is obtained from Eq. (10.35):

[latex] \begin{aligned} \sigma_{m} & =\frac{P}{A}\left[1+\frac{e c}{r^{2}} \sec \left(\frac{\pi}{2} \sqrt{\frac{P}{P_{ ext {cr }}}} ight) ight] \ & =\frac{31.1 \mathrm{kips}}{3.54 \mathrm{in}^{2}}\left[1+\frac{(0.75 \mathrm{in} .)(2 \mathrm{in} .)}{(1.50 \mathrm{in} .)^{2}} \sec \left(\frac{\pi}{2 \sqrt{2}} ight) ight] \ & =(8.79 \mathrm{ksi})[1+0.667(2.252)] \quad \sigma_{m}=22.0 \mathrm{ksi} \end{aligned} [/latex]

Question 10.SP.2: The uniform column AB consists of an 8-ft section of structu...

Related Answered Questions

An aluminum column of length L and rectangular cross section has a fixed end B and ...

Verified Answer:

A steel column having an effective length of 16 ft is loaded eccentrically as shown. ...

Verified Answer:

Determine the longest unsupported length L for which the S100 × 11.5 rolled-steel ...

Verified Answer:

Using the interaction method, solve Sample Prob. 10.5. Assume (σall)bending = 150 MPa. ...

Verified Answer:

Using the allowable-stress method, determine the largest load P that can be safely ...

Verified Answer:

Column AB consists of a W10 × 39 rolled-steel shape made of a grade of steel for which ...

Verified Answer:

Using the aluminum alloy 2014-T6, determine the smallest diameter rod that can be used ...

Verified Answer:

Use the interaction method to determine the maximum load P that can be safely ...

Verified Answer:

A column with a 2-in.-square cross section and 28-in. effective length is made of the ...

Verified Answer:

Knowing that column AB (Fig. 10.31) has an effective length of 14 ft, and that it must ...

Verified Answer: