Question 16.1: The vertical pressure vessel shown in Figure 16.4 has the fo...
The vertical pressure vessel shown in Figure 16.4 has the following design values:
Total weight=252,000 lbs
T =0.088 s (obtained from Example 16.3 in Section 16.2.2)
I_{p} =1.0
Location: vicinity of Portland, Oregon.
Base of the vessel is at ground level (z =0.0).
Site class is B (rock foundation): F_{a} =1.0
Determine the earthquake lateral load using the ASD method and
- a) Equation (16.2)
F_{ p }=0.4 I_{ p } S_{ DS } W_{ p }(1+2 z / h) (16.2)
- b) Equation (16.4).
F_{ p }=0.4 I_{ p } S_{ a } W_{ p }(1+2 z / h) (16.4)
a)
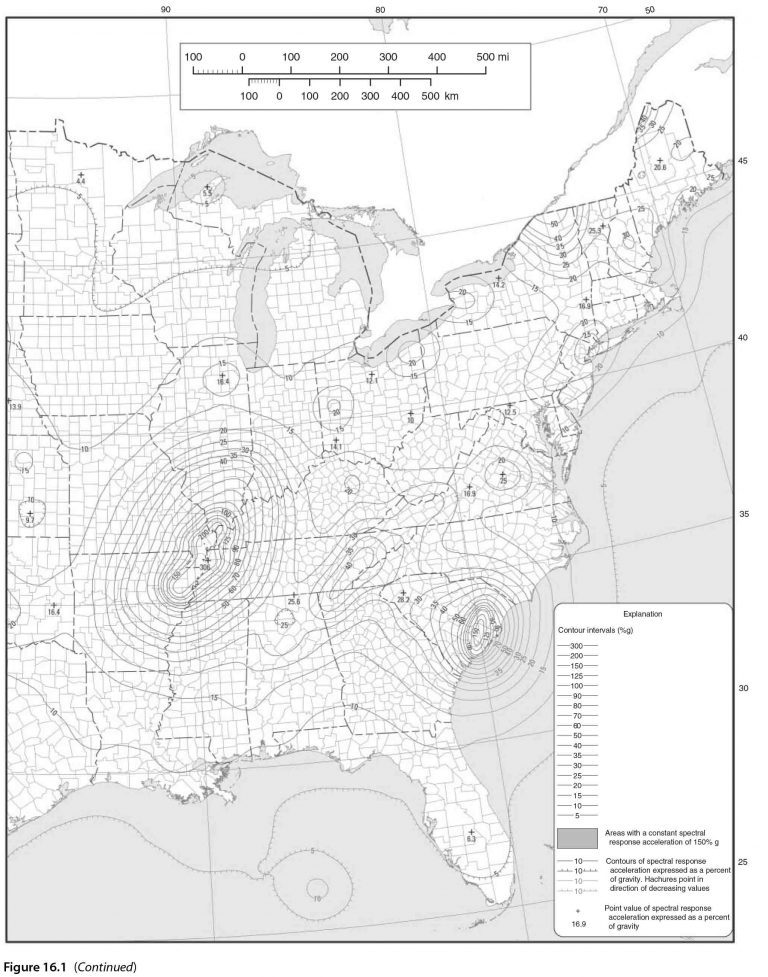
S_{s} = 0.9 from Figure 16.1.
From Eq. (16.3),
S_{ DS }=0.667 F_{ a } S_{ s } (16.3)
S_{DS} = 0.667(1)(0.9) = 0.6
From Eq. (16.2),
F_{ p }=0.4 I_{ p } S_{ DS } W_{ p }(1+2 z / h) (16.2)
F_{p} = (2∕3)[0.4(1)(0.6)(252,000)(1)]
= 0.16(252,000)
= 40,320 lbs = 1344 lbs∕ft of length.
S_{1} = 0.5 from Figure 16.2
T_{L} = 16 from Figure 16.3
T_{s} = 0.5∕0.9 = 0.556
T_{o} = 0.2(0.556) = 0.111.
Since T is less than T_{o}, Eq. (16.5a) is used
S_{ a }=S_{ DS }\left(0.4+0.6 T / T_{ o }\right) \quad T<T_{ o } (16.5a)
S_{a} = (0.6)[0.4 + 0.6(0.088)∕0.111] = 0.525.
From Eq. (16.4),
F_{ p }=0.4 I_{ p } S_{ a } W_{ p }(1+2 z / h) (16.4)
F_{ p } = (2∕3)[0.4(1)(0.525)(252,000)(1)]
= 0.14(252,000)
= 35,280 lbs = 1176 lbs∕ft.
A software program and maps may be accessed for determining the values of S_{s} and S_{1} more accurately at the USGS Website “http://earthquake.usgs.gov/hazards/ designmaps/” based on the address of the vessel location.
