Question 3.SP.10: Three cables are attached to a bracket as shown. Replace the...
Three cables are attached to a bracket as shown. Replace the forces exerted by the cables with an equivalent force-couple system at A.
STRATEGY: First determine the relative position vectors drawn from point A to the points of application of the various forces and resolve the forces into rectangular components. Then, sum the forces and moments.

Learn more on how we answer questions.
MODELING and ANALYSIS: Note that \pmb{F}_B=(700 N) \pmb{\lambda}_{BE} where
\pmb{\lambda}_{B E}=\frac{\overrightarrow{B E}}{B E}=\frac{75 \pmb{i}-150 \pmb{j}+50 \pmb{k}}{175}Using meters and newtons, the position and force vectors are
\begin{aligned}\pmb{r}_{B / A} &=\overrightarrow{A B}=0.075 \pmb{i}+0.050 \pmb{k} & \pmb{F}_B=300 \pmb{i}-600 \pmb{j}+200 \pmb{k} \\\pmb{r}_{C / A} &=\overrightarrow{A C}=0.075 \pmb{i}-0.050 \pmb{k} & \pmb{F}_C=707 \pmb{i} \quad-707 \pmb{k} \\\pmb{r}_{D / A} &=\overrightarrow{A D}=0.100 \pmb{i}-0.100 \pmb{j} & \pmb{F}_D=600 \pmb{i}+1039 \pmb{j}\end{aligned}The force-couple system at A equivalent to the given forces consists of a force R = ΣF and a couple \pmb{M}_A^R=\Sigma(\pmb{r} \times \pmb{F}). Obtain the force R by adding respectively the x, y, and z components of the forces:
R = ΣF =(1607 N)i +(439 N)j −(507 N)k
The computation of \pmb{M}_A^R is facilitated by expressing the moments of the forces in the form of determinants (Sec. 3.1F). Thus,
\pmb{r}_{B / A} \times \pmb{F}_B=\left|\begin{array}{ccc}\pmb{i} & \pmb{j} & \pmb{k} \\ 0.075 & 0 & 0.050 \\ 300 & -600 & 200\end{array}\right|=30 \pmb{i} \quad-45 \pmb{k}\pmb{r}_{C / A} \times \pmb{F}_C=\left|\begin{array}{ccc}\pmb{i} & \pmb{j} & \pmb{k} \\ 0.075 & 0 & -0.050 \\ 707 & 0 & -707\end{array}\right|=17.68 \pmb{j}
\pmb{r}_{D / A} \times \pmb{F}_D=\left|\begin{array}{ccc}\pmb{i} & \pmb{j} & \pmb{k} \\ 0.100 & -0.100 & 0 \\ 600 & 1039 & 0\end{array}\right|=\quad 163.9 \pmb{k}
Adding these expressions, you have
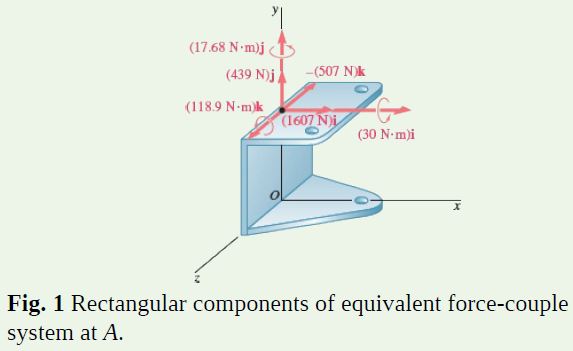
\pmb{M}_A^R=\Sigma(\pmb{r} \times \pmb{F})=(30 N \cdot m) \pmb{i}+(17.68 N \cdot m) \pmb{j}+(118.9 N \cdot m) \pmb{k}Figure 1 shows the rectangular components of the force R and the couple \pmb{M}_A^R.
REFLECT and THINK: The determinant approach to calculating moments shows its advantages in a general three-dimensional problem such as this.