Question 17.19: Two links of equal length ‘l’ are hinged and arranged vertic...
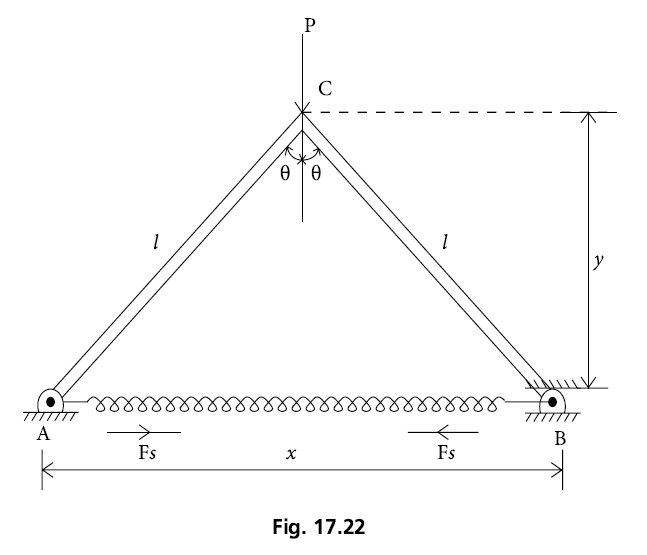
Two links of equal length ‘l’ are hinged and arranged vertically as shown in Fig. 17.22. They are connected at their lower ends by un–stretched spring of length ‘s’. When a vertical force ‘p’ is applied, determine the spring constant ‘k’ to maintain equilibrium at the position shown.
[MTU 2013–14]
Initial length of spring = s
Let the spring is stretched when both links make angle θ from vertical axis.
Final length of spring aſter stretching will be given by = 2lsinθ
Stretched amount along AB of spring = (2lsinθ–s)
i.e., x = (2lsinθ –s)
And y = lcosθ
If force ‘p’ moves down by virtual distance ‘\delta y’ and force in spring is F_{s},
\delta x = 2lcosθ.\delta \theta and \delta y = – lsinθ.\delta \theta
Using principle of virtual work,
P(+\delta y) + F_{s} (–\delta x) = 0
P(lsinθ.\delta \theta) + k(2lsinθ–s)(2lcosθ\delta \theta) = 0
Psinθ = k (2lsinθ –s) \times 2 cosθ
k=\frac{P \cdot \tan \theta}{2(2 l \sin \theta-s)}