Question 10.10: What is the minimum required thickness of a ring flange with...
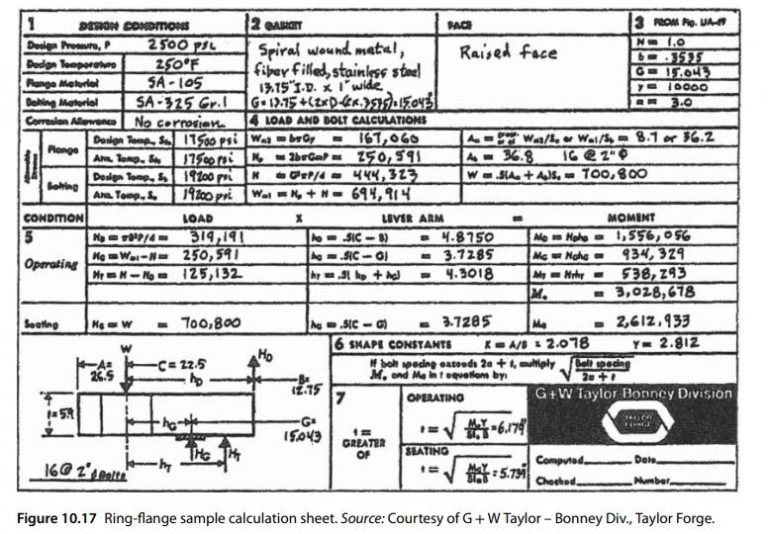
What is the minimum required thickness of a ring flange with the same design data as given in Example 10.9? The inside diameter has been increased to fit over the outside of the shell to where B=12.75 in. The bolt loadings and bolt size are the same as mentioned in Example 10.9. A sample calculation sheet is shown in Figure 10.17.
1) Calculate the total flange moment for design condition. Flange loads:
H_{ D }=\frac{\pi}{4} B^{2} P=\frac{\pi}{4}(12.75)^{2}(2500) =319,200
H_{ D }=H_{ p } =250,600
H_{ T }=H-H_{ D } = 444,300 − 319,200 = 125,100.
Lever arms:
h_{ D } = 0.5(C − B) = 0.5(22.5 − 12.75) = 4.875in.
h_{G} = 0.5(C − G) = 0.5(22.5 − 15.043) = 3.729in.
h_{T} = 0.5(h_{D} + h_{G}) = 0.5(4.875 + 3.729) = 4.302in.
Flange moments:
M_{D} = H_{D} × h_{D} = (319,200)(4.875) = 1,556,000
M_{G} = H_{G} × h_{G} = (250,600)(3.729) = 934,500
M_{T} = H_{T} × h_{T} = (125,100)(4.302) = 538,200
M_{dc} = M_{D} + M_{G} + M_{T} = 3,029,000.
2) Bolt-up moment is the same as mentioned in Example 10.9, M_{BU} =2,613,000.
3) Shape constants are K =A/B=26.5/12.75=2.078. From Figure 2-7.1 of the ASME Code, VIII-1, Y =2.812.
4) Required thickness based on design condition is
t=\sqrt{\frac{M_{ dc } Y}{S_{ f } B}}=\sqrt{\frac{(3,029,000)(2.812)}{(17,500)(12.75)}}=6.179 in