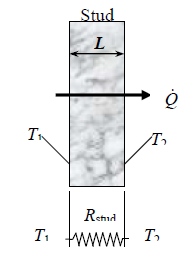
A 10-cm-thick wall is to be constructed with 2.5-m long wood studs ( k = 0.11 W / m \cdot{ }^{\circ} C ) that have a cross section of 10 cm \times 10 cm. At some point the builder ran out of those studs and started using pairs of 2.5-m-long wood studs that have a cross section of 5 cm \times 10 cm nailed to each other instead. The manganese steel nails (k = 50 W / m \cdot{ }^{\circ} C) are 10 cm long and have a diameter of 0.4 cm. A total of 50 nails are used to connect the two studs, which are mounted to the wall such that the nails cross the wall. The temperature difference between the inner and outer surfaces of the wall is 8°C. Assuming the thermal contact resistance between the two layers to be negligible, determine the rate of heat transfer (a) through a solid stud and (b) through a stud pair of equal length and width nailed to each other. (c) Also determine the effective conductivity of the nailed stud pair.
Question 3.54: A 10-cm-thick wall is to be constructed with 2.5-m long wood...
Learn more on how we answer questions.
A wall is to be constructed of 10-cm thick wood studs or with pairs of 5-cm thick wood studs nailed to each other. The rate of heat transfer through the solid stud and through a stud pair nailed to each other, as well as the effective conductivity of the nailed
stud pair are to be determined.
Assumptions 1 Heat transfer is steady since there is no indication of change with time. 2 Heat transfer can be approximated as being one-dimensional since it is predominantly in the x direction. 3 Thermal conductivities are constant. 4 The thermal contact resistance between the two layers is negligible. 4 Heat transfer by radiation is disregarded.
Properties The thermal conductivities are given to be k = 0.11 W / m \cdot{ }^{\circ} C for wood studs and k = 50 W / m \cdot{ }^{\circ} C for manganese steel nails.
Analysis (a) The heat transfer area of the stud is A = (0.1 m )(2.5 m ) = 0.25 m ^{2}. The thermal resistance and heat transfer rate through the solid stud are
R_{s t u d}=\frac{L}{k A}=\frac{0.1 m }{\left(0.11 W / m \cdot{ }^{\circ} C \right)\left(0.25 m ^{2}\right)}=3.636{ }^{\circ} C / W\dot{Q}=\frac{\Delta T}{R_{\text {stud }}}=\frac{8^{\circ} C }{3.636^{\circ} C / W }= 2 . 2 W
(b) The thermal resistances of stud pair and nails are in parallel
A_{\text {nails }}=50 \frac{\pi D^{2}}{4}=50\left[\frac{\pi(0.004 m )^{2}}{4}\right]=0.000628 m ^{2}R_{\text {nails }}=\frac{L}{k A}=\frac{0.1 m }{\left(50 W / m \cdot{ }^{\circ} C \right)\left(0.000628 m ^{2}\right)}=3.18^{\circ} C / W
R_{\text {stud }}=\frac{L}{k A}=\frac{0.1 m }{\left(0.11 W / m \cdot{ }^{\circ} C \right)\left(0.25-0.000628 m ^{2}\right)}=3.65^{\circ} C / W
\frac{1}{R_{\text {total }}}=\frac{1}{R_{\text {stud }}}+\frac{1}{R_{\text {nails }}}=\frac{1}{3.65}+\frac{1}{3.18} \longrightarrow R_{\text {total }}=1.70^{\circ} C / W
\dot{Q}=\frac{\Delta T}{R_{s t u d}}=\frac{8^{\circ} C }{1.70^{\circ} C / W }=4.7 W
(c) The effective conductivity of the nailed stud pair can be determined from
\dot{Q}=k_{e f f} A \frac{\Delta T}{L} \longrightarrow k_{e f f}=\frac{\dot{Q} L}{\Delta T A}=\frac{(4.7 W )(0.1 m )}{\left(8^{\circ} C \right)\left(0.25 m ^{2}\right)}=0.235 W / m \cdot{ }^{\circ} C