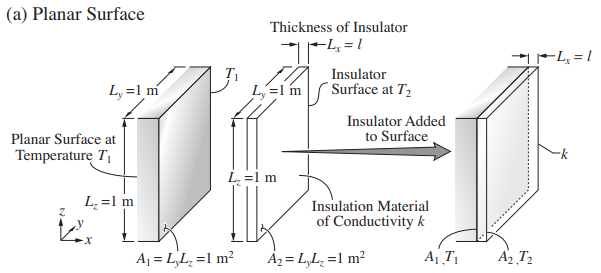
A1 m^{2} surface area designated as A_{1} is to be thermally insulated by placing an insulation of thickness l and conductivity k over it. The surface is at temperature T_{1} and the insulation surface is at temperature T_{2} . This 1 m^{2} surface area can be in the form of (a) a planar surface with area A_{1} = L_{y}L_{z} , (b) a cylindrical surface with area A_{1} = 2\pi R_{1}L_{y} , or (c) a spherical surface with area A_{1} = 4\pi R^{2}_{1}. These surfaces are shown in Figure, along with the geometry of their respective insulations. For the planar surface, we have L_{y} = L_{z} = 1 m, and for the cylindrical surface we have L_{y} = 1 m. The thickness of the insulation l = 5 cm and its conductivity k = 0.1 W/m-K. The temperatures are T_{1} = 90^{\circ }C and T2 = 40^{\circ }C. Determine the rate of heat loss from each surface and comment on any differences among them.
Question 3.6: A 1m^2 surface area designated as A1 is to be thermally insu...


Learn more on how we answer questions.
The three surfaces have the same surface area A_{1} = 1 m^{2} ; however the insulation surface away from A_{1} , i.e., A_{2} , is not the same for all the three geometries. The heat flow rate at the surface A_{1} with the insulation added is given by the appropriate resistance listed in Table. For the three cases, these are
(a) Q_{k,1-2}(planar)=\frac{T_{1}-T_{2}}{R_{k,1-2}(planar)}=\frac{T_{1}-T_{2}}{\frac{l}{A_{1}k} }=\frac{T_{1}-T_{2}}{\frac{l}{L_{y}L_{z}k} } Table
(b) Q_{k,1-2}(cylinder)=\frac{T_{1}-T_{2}}{R_{k,1-2}(cylinder)}=\frac{T_{1}-T_{2}}{\frac{ln(R_{2}/R_{1})}{2\pi Lk} }=\frac{T_{1}-T_{2}}{\frac{ln\frac{R_{1}+l}{R_{1}} }{2\pi L_{y}k} } Table
(c) Q_{k,1-2}(sphere)=\frac{T_{1}-T_{2}}{R_{k,1-2}(sphere)}=\frac{T_{1}-T_{2}}{\frac{\frac{1}{R_{1}}-\frac{1}{R_{2}} }{4\pi k} }=\frac{T_{1}-T_{2}}{\frac{\frac{1}{R_{1}}-\frac{1}{R_{1}+l} }{4\pi k} } Table
The inner radii, R_{1} , for the cylindrical and spherical geometries are determined from
A_{1}=1 m^{2}=2\pi R_{1}L_{z}=2\pi R_{1}(m)\times 1(m) or R_{1}(cylinder)= 0.1590 mA_{1}=1 m^{2}=4\pi R_{1}^{2} or R_{1}(sphere)= 0.2822 m
Using the numerical values for k and l, along with Ly, Lz, and R1, we have
(a) Q_{k,1-2}(planar)= \frac{50 (^{\circ }C)}{\frac{ 0.05(m)}{0.1(W/m-^{\circ }C)\times 1(m)\times 1(m)}}=100.0 W
(b) Q_{k,1-2}(cylinder)= \frac{50 (^{\circ }C)}{\frac{ ln \left[\frac{0.159(m)+0.05(m)}{0.159(m)} \right] }{2\pi \times 0.1(W/m-^{\circ }C)\times 1(m)}}=114.8 W
(c) Q_{k,1-2}(sphere)= \frac{50 (^{\circ }C)}{\frac{ \frac{1}{0.2822(m)}-\frac{1}{0.2822(m)+0.05(m)} }{4\pi \times 0.1(W/m-^{\circ }C)}}=117.7 W
