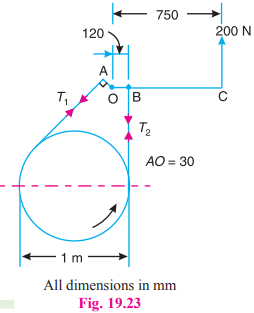
A band and block brake, having 14 blocks each of which subtends an angle of 15^{\circ} at the centre, is applied to a drum of 1 m effective diameter. The drum and flywheel mounted on the same shaft has a mass of 2000 kg and a combined radius of gyration of 500 mm. The two ends of the band are attached to pins on opposite sides of the brake lever at distances of 30 mm and 120 mm from the fulcrum. If a force of 200 N is applied at a distance of 750 mm from the fulcrum, find:
1. maximum braking torque, 2. angular retardation of the drum, and 3. time taken by the system to come to rest from the rated speed of 360 r.p.m.
The coefficient of friction between blocks and drum may be taken as 0.25.
Question : A band and block brake, having 14 blocks each of which subte...
Given : n = 14 ; 2 \theta=15^{\circ} \text { or } \theta=7.5^{\circ} ; d = 1 m or r = 0.5 m ; m = 2000 kg ; k = 500 mm = 0.5 m ; P = 200 N ; N = 360 r.p.m. ; l = 750 mm ; \mu = 0.25
1. Maximum braking torque
The braking torque will be maximum when OB > OA and the drum rotates anticlockwise as shown in Fig. 19.23. The force P must act upwards and the end of the band attached to A is tight under tension T_{1} and the end of the band attached to B is slack under tension T_{2}.
Taking moments about O,
200 \times 750+T_{1} \times 30=T_{2} \times 120
12 T_{2}-3 T_{1}=15000 …(i)
We know that \frac{T_{1}}{T_{2}}=\left(\frac{1+\mu \tan \theta}{1-\mu \tan \theta}\right)^{n}
=\left(\frac{1+0.25 \tan 7.5^{\circ}}{1-0.25 \tan 7.5^{\circ}}\right)^{14}
=\left(\frac{1+0.25 \times 0.1317}{1-.025 \times 0.1317}\right)^{14}
=(1.068)^{14}=2.512 …(ii)
From equations (i) and (ii),
T_{1}=8440 N , \text { and } T_{2}=3360 NWe know that maximum braking torque,
T_{ B }=\left(T_{1}-T_{2}\right) r=(8440-3360) 0.5=2540 N – m
2. Angular retardation of the drum
Let \alpha = Angular retardation of the drum.
We know that braking torque \left(T_{ B }\right),
2540=I . \alpha=m \cdot k^{2} \cdot \alpha=2000(0.5)^{2} \alpha=500 \alpha
\therefore \alpha=2540 / 500=5.08 rad / s ^{2}
3. Time taken by the system to come to rest
Let t = Required time.
Since the system is to come to rest from the rated speed of 360 r.p.m., therefore
Initial angular speed, \omega_{1}=2 \pi \times 360 / 60=37.7 rad / s
and final angular speed, \omega_{2}=0
We know that \omega_{2}=\omega_{1}-\alpha . t …(– ve sign due to retardation )
\therefore t=\omega_{1} / \alpha=37.7 / 5.08=7.42 s
