Question 2.43: A boat weighs 500,000 N and floats in water. Its horizontal ...

(a) In order to determine the buoyant force, F_{B} and the volume of the displaced fluid, V_{dispfluid } , one may apply Newton’s second law of motion for fluids in static equilibrium to the floating boat (body) in the vertical direction, which yields the following:

The V_{dispfluid } and the buoyant force, F_{B}= \gamma _{w} V_{dispfluid } dispfluid are determined as follows:

W: = 500.000 N                          \gamma _{w} :=9810 \frac{N}{m^{3}}

Guess value:                                  V_{dispfluid} = 10 m^{3}                          F_{B}:=1000000 N

Given

– W + F_{B} =0                                F_{B} = \gamma _{w} V_{dispfluid}
\left ( \begin{matrix} V_{dispfluid} \\ F_{B} \end{matrix} \right ) := Find ( V_{dispfluid},F_{B} )
V_{dispfluid} = 50.968 m^{3}                                    F_{B} = 5 \times 10^{5} N

(b) It may be noted that if the boat were bottom heavy (i.e., G is located below B), then the boat would always be in a position of rotational stable equilibrium. However, because the boat is top heavy (i.e., G is located above B), there is a maximum height for G above which the boat will be in a position of rotational unstable equilibrium (i.e., metacentric height, GM is negative). At the maximum height for G above B, the boat will be in a position of neutral (or marginal) equilibrium. This condition occurs when the metacentric height, GM is equal to zero. Thus, in order to determine the maximum distance GB that the center of gravity, G maybe above the center of buoyancy, B in order for the boat to be in a position of rotational stable equilibrium, one must set the metacentric height, GM equal to zero. Thus, the metacentric height, GM for the top-heavy floating boat is set equal to zero as follows:

GM= BM – GB = 0
BM = GB

The distance BM = (I_{y} V_{dispfluid }) ( I_{y} for rectangular and circular cross sections are given in Table B.1 in Appendix B) is computed as follows:

h:= 6 m                        b: = 20 m                       D: = 6 m
I_{yrectangle}: = \frac{b.h^{3}}{12} = 360 m^{4}                                    I_{ ycircle}: = \frac{\pi .D^{4}}{64} = 36.617 m^{4}
I_{ y}:= I_{yrectangle} + I_{ ycircle} = 423.617 m^{4}
BM: = \frac{ I_{ y}}{ V_{dispfluid} }

Thus, the maximum distance GB that the center of gravity, G may be above the center of buoyancy, B in order for the boat to be in a position of rotational stable equilibrium is:

Table B.1
The Area, A, the Center of Area (Centroid), y_{ca} and x_{ca} ,  the Centroidal Moment of Inertia, I_{x-ca} , and the Moment of Inertia about the y-Axis, I_{y} for Some Common Geometric Shapes
Shape	A	y_{ca}	x_{ca}	I_{x-ca}	I_{y}
	\frac{\pi BL}{4}	\frac{L}{2}		\frac{\pi BL^{3} }{64}	\frac{\pi B^{3}L }{16}
	\frac{\pi BL}{4}	\frac{4L}{3\pi }		\frac{\pi BL^{3} }{16}-\frac{4 BL^{3}}{9\pi }
	\frac{2 BL}{3}	\frac{3L}{5}	\frac{3B}{8}	\frac{\pi BL^{3} }{7}-\frac{18 BL^{3}}{75 }
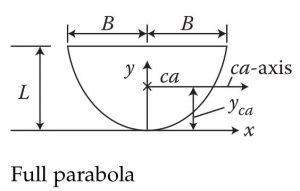	(\frac{2 BL}{3} )	\frac{3L}{5}		2(\frac{\pi BL^{3} }{7}-\frac{18 BL^{3}}{75 })