Question 5.10: A cantilever beam made of cold drawn steel 20C8 (Sut = 540 N...

\text { Given } P=\pm 1000 N \quad S_{u t}=540 N / mm ^{2} .

q = 0.85       R = 90%         N = 10 000 cycles.

Step I Selection of failure section
The failure will occur either at the section A or at the section B. At section A, although the bending moment is maximum, there is no stress concentration and the diameter is also more compared with that of the section B. It is, therefore, assumed that the failure will occur at the section B.

Step II Construction of S–N diagram

S_{e}^{\prime}=0.5 S_{u t}=0.5(540)=270 N / mm ^{2} .

\text { From Fig. } 5.24 \text { (cold drawn steel and } S_{u t}=\left.540 N / mm ^{2}\right) .

K_{a}=0.78 .

Assuming, 7.5 < d < 50 mm,

K_{b}=0.85 .

\text { For } 90 \% \text { reliability, } K_{c}=0.897 .

At the section B,

\left(\frac{D}{d}\right)=1.5 \text { and }\left(\frac{r}{d}\right)=0.25 .

\text { From Fig. } 5.5, \quad K_{t}=1.35 .

From Eq. (5.12),

K_{f}=1+q\left(K_{t}-1\right)                 (5.12).

K_{f}=1+q\left(K_{t}-1\right)=1+0.85(1.35-1)=1.2975 .

K_{d}=\frac{1}{K_{f}}=\frac{1}{1.2975}=0.771 .

S_{e}=K_{a} K_{b} K_{c} K_{d} S_{e}^{\prime} .

=0.78(0.85)(0.897)(0.771)(270)=123.8 N / mm ^{2} .

0.9 S_{u t}=0.9(540)=486 N / mm ^{2} .

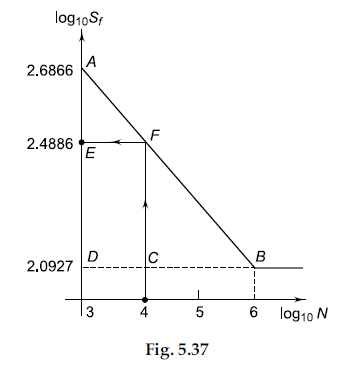
\log _{10}\left(0.9 S_{u t}\right)=\log _{10}(486)=2.6866 .

\log _{10}\left(S_{e}\right)=\log _{10}(123.8)=2.0927 .

\log _{10}(10000)=4 .

The S–N curve for this problem is shown in Fig. 5.37.

Step III Diameter of beam

From Fig. 5.37,

\overline{A E}=\frac{\overline{A D} \times \overline{E F}}{\overline{D B}}=\frac{(2.6866-2.0927)(4-3)}{(6-3)}=0.198 .

Therefore,

\log _{10} S_{f}=2.6866-\overline{A E}=2.6866-0.198=2.4886 .

S_{f}=308.03 N / mm ^{2} .

S_{f}=\sigma_{b}=\frac{32 M_{b}}{\pi d^{3}} .

d^{3}=\frac{32 M_{b}}{\pi S_{f}}=\frac{32(1000 \times 150)}{\pi(308.03)}.

d = 17.05 mm.