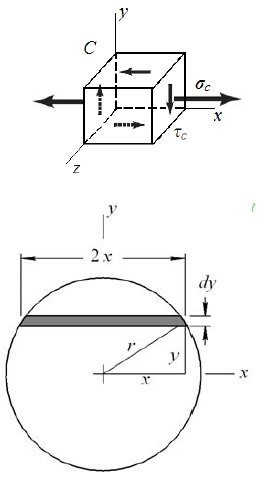
A cantilever beam with a 1-in-diameter round cross section is loaded at the tip with a tr verse force of 1000 lbf, as shown in the figure. The cross section at the wall is also shown, with labeled points A at the top, B at the center, and C at the midpoint between A and B. Study the

Question

A cantilever beam with a 1-in-diameter round cross section is loaded at the tip with a tr verse

force of 1000 lbf, as shown in the figure. The cross section at the wall is also shown, with

labeled points A at the top, B at the center, and C at the midpoint between A and B. Study the

significance of the tr verse shear stress in combination with bending by performing the following steps.

(a) Assume [latex]L=10 [/latex]in. For points [latex]A, B [/latex] and [latex]C [/latex] sketch three-dimensional stress elements, labeling the coordinate directions and showing all stresses. Calculate magnitudes of the stresses on the stress elements. Do not neglect tr verse shear stress. Calculate the maximum shear stress for each stress element.

(b) For each stress element in part ( a), calculate the maximum shear stress if the tr verse shear stress is neglected. Determine the percent error for each stress element from neglecting the tr verse shear stress.

( [latex]c [/latex]) Repeat the problem for [latex]L=4,1 [/latex] and [latex]0.1 [/latex]in. Compare the results and state any conclusions regarding the significance of the tr verse shear stress in combination with bending.

Accepted Answer

(a) [latex]L=10 [/latex]in. Element [latex]A [/latex]:

[latex]\begin{aligned}&\sigma_{A}=-\frac{M y}{I}=-\frac{-(1000)(10)(0.5)}{(\pi / 64)(1)^{4}}\left(10^{-3}\right)=101.9 \mathrm{kpsi} \&\tau_{A}=\frac{V Q}{I b}, \quad Q=0 \Rightarrow \tau_{A}=0 \&\tau_{\max }=\sqrt{\left(\frac{\sigma_{A}}{2}\right)^{2}+\tau_{A}^{2}}=\sqrt{\left(\frac{101.9}{2}\right)^{2}+(0)^{2}}=50.9 \mathrm{kpsi} \quad \text { . }\end{aligned} [/latex]

Element [latex]B [/latex]:

[latex]\begin{aligned}&\sigma_{B}=-\frac{M y}{I}, \quad y=0 \quad \Rightarrow \quad \sigma_{B}=0 \&Q=\bar{y}^{\prime} A^{\prime}=\left(\frac{4 r}{3 \pi}\right)\left(\frac{\pi r^{2}}{2}\right)=\frac{4 r^{3}}{6}=\frac{4(0.5)^{3}}{6}=1 / 12 \mathrm{in}^{3}\end{aligned}\ [/latex].

[latex]\begin{gathered}\tau_{B}=\frac{V Q}{I b}=\frac{(1000)(1 / 12)}{(\pi / 64)(1)^{4}(1)}\left(10^{-3}\right)=1.698 \mathrm{kpsi} \ \tau_{\max }=\sqrt{\left(\frac{0}{2}\right)^{2}+1.698^{2}}=1.698 \mathrm{kpsi} \quad \text { }\end{gathered}\ [/latex]

Element [latex]C [/latex]:

[latex]\ \begin{aligned}&\sigma_{C}=-\frac{M y}{I}=-\frac{-(1000)(10)(0.25)}{(\pi / 64)(1)^{4}}\left(10^{-3}\right)=50.93 \mathrm{kpsi} \&Q=\int_{y1}^{r} y d A=\int_{y1}^{r} y(2 x) d y=\int_{y1}^{r} y\left(2 \sqrt{r^{2}-y^{2}}\right) d y \&\quad=-\left.\frac{2}{3}\left(r^{2}-y^{2}\right)^{3 / 2}\right|_{y 1} ^{r}=-\frac{2}{3}\left[\left(r^{2}-r^{2}\right)^{3 / 2}-\left(r^{2}-y_{1}^{2}\right)^{3 / 2}\right] \&\quad=\frac{2}{3}\left(r^{2}-y_{1}^{2}\right)^{3 / 2}\end{aligned} [/latex]

For [latex]C, y_{1}=r / 2=0.25 [/latex]in

[latex]\begin{gathered}Q=\frac{2}{3}\left(0.5^{2}-0.25^{2}\right)^{3 / 2}=0.05413 \mathrm{in}^{3} \b=2 x=2 \sqrt{r^{2}-y_{1}^{2}}=2 \sqrt{0.5^{2}-0.25^{2}}=0.866 \mathrm{in} \ \tau_{C}=\frac{V Q}{I b}=\frac{(1000)(0.05413)}{(\pi / 64)(1)^{4}(0.866)}\left(10^{-3}\right)=1.273 \mathrm{kpsi}\end{gathered}\ [/latex][latex]\tau_{\max }=\sqrt{\left(\frac{50.93}{2}\right)^{2}+(1.273)^{2}}=25.50 \mathrm{kpsi} [/latex]

(b) Neglecting transverse shear stress:

Element [latex]A [/latex]: Since the tr verse shear stress at point [latex]A [/latex]is zero, there is no change. [latex]\tau_{\max }=50.9 \mathrm{kpsi} [/latex]

[latex]\% [/latex]error [latex]=0 \% [/latex].

Element [latex]B [/latex]: Since the only stress at point [latex]B [/latex]is tr verse shear stress, neglecting the tr verse shear stress ignores the entire stress.

[latex]\begin{aligned}&\tau_{\max }=\sqrt{\left(\frac{0}{2}\right)^{2}}=0 \text { psi } \text { } \&\% \text { error }=\left(\frac{1.698-0}{1.698}\right) *(100)=100 \% \text { . }\end{aligned}\[/latex]

Element [latex]C [/latex]:

[latex]\begin{aligned}&\tau_{\max }=\sqrt{\left(\frac{50.93}{2}\right)^{2}}=25.47 \mathrm{kpsi} \quad \text { . } \&\% \text { error }=\left(\frac{25.50-25.47}{25.50}\right) *(100)=0.12 \% \quad \text { }\end{aligned} [/latex]

(c) Repeating the process with different beam lengths produces the results in the table.

[latex]\begin{array}{|c|c|c|c|c|c|}\hline & \begin{array}{c}\text { Bending } \ \text { stress, } \ \sigma(\mathrm{kpsi})\end{array} & \begin{array}{c}\text { Tr verse } \ \text { shear stress, } \ \tau(\mathrm{kpsi})\end{array} & \begin{array}{c}\text { Max shear } \ \text { stress, } \ \tau_{\max }(\mathrm{kpsi})\end{array} & \begin{array}{c}\text { Max shear } \ \text { stress, } \ \text { neglecting } \tau, \ \tau_{\max }(\mathrm{kpsi})\end{array} & \% \text { error } \ \hline \boldsymbol{L}=\mathbf{1 0} \text { in } & & & & & \ \hline A & 102 & 0 & 50.9 & 50.9 & 0 \ \hline B & 0 & 1.70 & 1.70 & 0 & 100 \ \hline C & 50.9 & 1.27 & 25.50 & 25.47 & 0.12 \ \hline L=\mathbf{4} \text { in } & & & & & \ \hline A & 40.7 & 0 & 20.4 & 20.4 & 0 \ \hline B & 0 & 1.70 & 1.70 & 0 & 100 \ \hline \mathrm{C} & 20.4 & 1.27 & 10.26 & 10.19 & 0.77 \ \hline L=\mathbf{1} \text { in } & & & & & \ \hline A & 10.2 & 0 & 5.09 & 5.09 & 0 \ \hline B & 0 & 1.70 & 1.70 & 0 & 100 \ \hline \mathrm{C} & 5.09 & 1.27 & 2.85 & 2.55 & 10.6 \ \hline L=\mathbf{0 . 1} \text { in } & & & & & \ \hline A & 1.02 & 0 & 0.509 & 0.509 & 0 \ \hline B & 0 & 1.70 & 1.70 & 0 & 100 \ \hline \mathrm{C} & 0.509 & 1.27 & 1.30 & 0.255 & 80.4 \ \hline\end{array}[/latex]

Discussion:

The tr verse shear stress is only significant in determining the critical stress element as the length of the cantilever beam becomes smaller. As this length decreases, bending stress reduces greatly and tr verse shear stress stays the same. This causes the critical element location to go from being at point [latex]A [/latex] on the surface, to point [latex]B [/latex] in the center. The maximum shear stress is on the outer surface at point [latex]A [/latex]for all cases except [latex]L=0.1 [/latex]in, where it is at point [latex]B [/latex]at the center. When the critical stress element is at point [latex]A [/latex] there is no error from neglecting tr verse shear stress, since it is zero at that location.

Neglecting the tr verse shear stress has extreme significance at the stress element at the center at point [latex]B [/latex] but that location is probably only of practical significance for very short beam lengths.

Question 3.45: A cantilever beam with a 1-in-diameter round cross section ...

Related Answered Questions