A cantilever spring made of 10 mm diameter wire is shown in Fig. 5.46. The wire is made of stainless steel 4Cr18Ni10 (Sut = 860 N/mm2 and Syt = 690 N/mm2). The force P acting at the free end varies from 75 N to 150 N. The surface finish of the wire is equivalent to the machined surface. There is

Question

A cantilever spring made of 10 mm diameter wire is shown in Fig. 5.46. The wire is made of stainless steel 4Cr18Ni10 [latex] \left(S_{u t}=860 N / mm ^{2}\right. [/latex] and [latex] \left.S_{y t}=690 N / mm ^{2}\right) [/latex]. The force P acting at the free end varies from 75 N to 150 N. The surface finish of the wire is equivalent to the machined surface. There is no stress concentration and the expected reliability is 50%. Calculate the number of stress cycles likely to cause fatigue failure.

Accepted Answer

Given For cantilever spring, d = 10 mm.

[latex] l=500 mm \quad P=75 ext { to } 150 N \quad S_{u t}=860 N / mm ^{2} [/latex].

[latex] S_{y t}=690 N / mm ^{2} \quad R=50 \% [/latex].

Step I Endurance limit stress for cantilever beam

[latex] S_{e}^{\prime}=0.5 S_{u t}=0.5(860)=430 N / mm ^{2} [/latex].

From Fig. 5.24 (machined surface and [latex] S_{u t}=860 \left. N / mm ^{2} ight)[/latex].

[latex] K_{a}=0.72 [/latex].

[latex] ext { For } 10 mm ext { diameter wire, } K_{b}=0.85 [/latex].

For 50% reliability,

[latex] K_{c}=1.0 [/latex].

[latex] S_{e}=K_{a} K_{b} K_{c} S_{e}^{\prime} [/latex].

[latex] =0.72(0.85)(1.0)(430)=263.16 N / mm ^{2} [/latex].

[latex] \left(M_{b} ight)_{\max .}=150 imes 500=75000 N - mm [/latex].

[latex] \left(M_{b} ight)_{\min .}=75 imes 500=37500 N - mm [/latex].

[latex] \left(M_{b} ight)_{m}=\frac{1}{2}\left[\left(M_{b} ight)_{\max .}+\left(M_{b} ight)_{\min .} ight] [/latex].

[latex] =\frac{1}{2}[75000+37500]=56250 N - mm [/latex].

[latex] \left(M_{b} ight)_{a}=\frac{1}{2}\left[\left(M_{b} ight)_{\max .}-\left(M_{b} ight)_{\min .} ight] [/latex].

[latex] =\frac{1}{2}[75000-37500]=18750 N - mm [/latex].

[latex] \sigma_{m}=\frac{32\left(M_{b} ight)_{m}}{\pi d^{3}}=\frac{32(56250)}{\pi(10)^{3}}=572.96 N / mm ^{2} [/latex].

[latex] \sigma_{a}=\frac{32\left(M_{b} ight)_{a}}{\pi d^{3}}=\frac{32(18750)}{\pi(10)^{3}}=190.99 N / mm ^{2} [/latex].

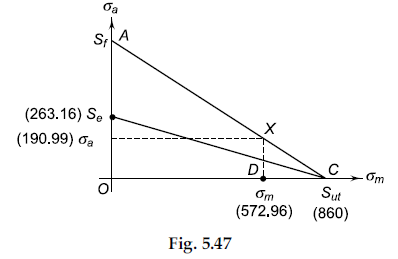
The modified Goodman diagram for this example is shown in Fig. 5.47. The point X with coordinates (572.96, 190.99) falls outside the region of safety.
This indicates a finite life for the spring. The value of [latex]S_{f}[/latex] is obtained by joining C to X and then extending the line to the ordinate. Point A gives the value of [latex]S_{f}[/latex].
From similar triangles XDC and AOC,

[latex] \frac{\overline{X D}}{\overline{A O}}=\frac{\overline{D C}}{\overline{O C}} [/latex].

[latex] S_{f}=\overline{A O}=\frac{\overline{X D} imes \overline{O C}}{\overline{D C}}=\frac{190.99(860)}{(860-572.96)} [/latex].

[latex] =572.22 N / mm ^{2} [/latex].

Step III Construction of S–N diagram

[latex] 0.9 S_{u t}=0.9(860)=774 N / mm ^{2} [/latex].

[latex] \log _{10}\left(0.9 S_{u t} ight)=\log _{10}(774)=2.8887 [/latex].

[latex] \log _{10}\left(S_{e} ight)=\log _{10}(263.16)=2.4202 [/latex].

[latex] \log _{10}\left(S_{f} ight)=\log _{10}(572.22)=2.7576 [/latex].

The S–N curve for this problem is shown in Fig. 5.48.

Step IV Fatigue life of cantilever spring From Fig. 5.48,

[latex] \overline{E F}=\frac{\overline{D B} imes \overline{A E}}{\overline{A D}}=\frac{(6-3)(2.8887-2.7576)}{(2.8887-2.4202)} [/latex].

[latex] =0.8395 [/latex].

[latex] \log _{10} N=3+\overline{E F}=3+0.8395=3.8395 [/latex].

N = 6910.35 cycles.

Question 5.15: A cantilever spring made of 10 mm diameter wire is shown in ...

Related Answered Questions